Конечный потенциальный барьер

Потенциальная энергия имеет вид:

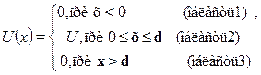Ясно, что происходит при Е 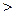U : с некой вероятностью частица может

отразиться от барьера. Наиболее интересен случай Е 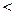U (рис. 30.3).Мы видели, что интенсивность (квадрат модуля амплитуды) волны убы-вает под барьером и на расстоянии (I становится меньше в ехр( ---2dk) раз.Но в этой точке барьер кончается, так что волна выйдет на свободу суменьшенной амплитудой. Отношение интенсивностей выходящей и па-дающей волн называется коэффициентом прозрачности D (он же равен

30.7. Отражение и туннелирование частиц

147

вероятности прохождения через барьер). Из наших рассуждений следуетприближенное выражение для него:

Получая D, мы опустили некие множители перед экспонентой, что пофизическому смыслу означает пренебрежение процессами, когда частица,прежде чем выйти из-под барьера, испытает многократное отражениеот его стенок. При высоком и широком барьере (D 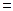1) вклад такихпроцессов невелик и сделанное приближение оправдано.

Проникновение частицы сквозь конечный потенциальный барьер воз-можно в квантовой механике, но категорически запрещено классической.В самом деле, формально вектор hк играет роль импульса (мнимого),так что кинетическая энергия Т=-h2к2/2m становится отрицатель-ной. Дело спасают соотношения неопределенностей. Модуль (мнимой)скорости частицы имеет порядок v?hк/т,так что время туннелиро-вания 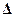t?dт/hk. Неопределенность в ``кинетической'' энергии 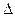Т ?h/2 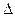t?h2к/2dm. Из полученных результатов для коэффициента про-зрачности видно, что эффект туннелирования заметен, если kd 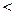1. Нотогда

Получается, что неопределенность в кинетической энергии частицы подбарьером больше самого значения кинетической энергии. Поэтому нельзяутверждать, что под барьером кинетическая энергия отрицательна. Ско-рее, она ``размыта'' настолько, что частица может как бы перепрыгнутьне слишком большой барьер. В случае же высокого и широкого барьера``размытость'' кинетической энергии должна быть очень велика, что воз-можно лишь на очень короткое время, за которое частица не успеваетпроскочить за барьер. Поэтому в этом случае коэффициент прозрачно-сти становится экспоненциально малым. По-другому: туннелированиезаметно при ширине барьера порядка длины волны де Бройля.

Барьер произвольной формы можно представить в виде последователь-ности прямоугольных барьеров; теорема об умножении вероятностей ве-дет к появлению суммы (интеграла) в экспоненте, так что вместо имеем

D?exp(-2kd) =exp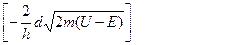

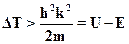
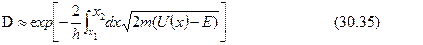
Глава 30. Уравнение Шредингера

Рис. 30.4: Частица в потенциальной яме, образованной непроницаемым препятствиеми конечным барьером

Интеграл берется между точками поворота (U ( 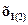) = Е), в которыхклассическая частица должна изменить направление движения.

Задача 30.23.Электрон находится в одномерной потенциальной яме ши-риной а = Ю-10 м (рис. 30.4) и имеет энергию Е= 1.5 эВ. С одной сто-роны ямы потенциальная энергия V(х) бесконечна, а с другой сторонывыйти из ямы электрону мешает потенциальный барьер высотой U = 2эВ и шириной d = 3 10-10 м. Оценить время жизни 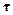электрона в яме.

Решение.Скорость электрона в яме v= 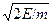и за промежутоквремени t он подойдет к барьеру vt/2а раз. При каждом подходе веро-ятность туннелирования равна так что вероятность туннелирования 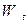за время t равна

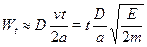
Вероятность 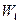увеличивается с ростом промежутка времени t. Принекотором значении t = 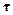вероятность туннелирования станет равнойединице и электрон вырвется из ямы. Отсюда получаем для временижизни электрона в яме оценку:

Теперь остается подставить численные данные. Для упрощения вычи-слений имеет смысл отдельно рассчитать коэффициент прозрачности ипред экспоненциальный множитель. Имеем:

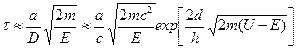
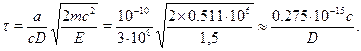
30.7. Отражение и туннелирование частиц

149

Теперь осталось рассчитать коэффициент прозрачности:

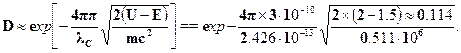
Получаем окончательно:

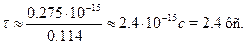
Даже по масштабам микромира это время мало: прежде чем электронпросочится сквозь барьер свет успеет пройти расстояние всего лишь в0.7 мкм. ¦

Прозрачность барьера сильно зависит от энергии частицы в яме и отширины и высоты барьера. Например, при увеличении ширины барьерав два раза новый коэффициент прозрачности будет равен, как легко до-гадаться, квадрату старого. Для электрона тогда получится значениеD = 0.0013 и его время жизни в яме увеличится до 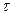= 21 фс. Это иобъясняет отсутствие туннелирования в обычном мире с его высокими иширокими потенциальными барьерами.

Задача 30.24.Решить предыдущую задачу, если вместо электрона в туже яму помещен протон.

Решение.Чтобы не решать аналогичную задачу с самого начала, можновоспользоваться результатами предыдущей. Протон массивнее электронав п = 1836 раз. В коэффициент прозрачности масса частицы входитпод квадратным корнем в показателе экспоненты. При изменении массыв п раз в показателе экспоненты появится множитель 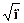и новый ко-эффициент прозрачности будет равен старому, возведенному в степень 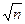= 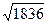?42.85. Используя данные предыдущей задачи, получаем

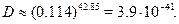
Предэкспоненциальный множитель также умножится на л/п и время жизнипротона в потенциальной яме будет равно

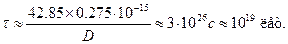
Глава 30. Уравнение Шредингера

Получилась столь огромная величина, что протон будет жить в ямевечно: время существования Вселенной ``всего'' 15 млрд лет. ¦

Эти две задачи демонстрируют сильную зависимость проницаемостибарьера от массы частицы.

• Оптическая аналогия прохождения частицы надбарьером

В этом разделе мы покажем, что прохождение квантовой частицы черезнизкий потенциальный барьер аналогично отражению света на границедвух полубесконечных сред. Далее, прохождение частицы через потенци-альный барьер конечной ширины может быть описано как множественноеотражение классических волн, и в результате опять-таки мы придем кизвестным результатам оптики. Целью данного раздела является демон-страция тесной связи различных областей физики.