Прохождение света через многослойную структуру
В этом разделе мы рассмотрим прохождение частицы над потенциаль-ным барьером, составленным из N прямоугольных конечных барьеровшириной d, причем межбарьерное расстояние всюду одинаково и равно b(рис. 30.7).
Рис. 30.7: Многослойная структура с периодом l=d+b, образованная N прямоуголь-ными потенциальными барьерами шириной d и межбарьерным расстоянием b.
В принципе решение задачи о нахождении коэффициента прохождения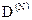 
через такой барьер может быть решена описанными выше спосо-бами. Сейчас нам важно только понять основной физический результат,так что нижеследующие формулы приводятся без вывода и только длясправки. Выражение для коэффициента прохождения имеет вид:
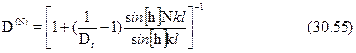
Глава 30. Уравнение Шредингера
Где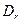 
--- коэффициент прохождения через одиночный прямоугольныйбарьер, вычисленный выше (при N= 1 получаем из 
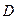= Dг).
Величина k называется квазиволновым вектором (для отличия от вол-новых векторов частицы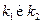 
и мы набираем ее прямым шрифтом).
В случае света мы используем для Dr результат . Связь квази-волнового вектора с частотой падающего света и показателем преломле-ния дается тогда выражением:
где
kl=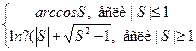 
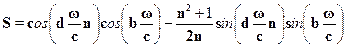
Наконец, входящие в функции определены как
sin[h]x=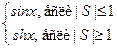 
Ясно, что для частот, при которых абсолютно прозрачен прямоуголь-ный барьер (Dг = 1), будет прозрачен и наш составной барьер (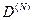 
= 1в этом случае, как следует и из формулы ). В дополнение по-явятся и новые окна прозрачности. Здесь ситуация очень похожа наслучай с дифракционной решеткой (см. Ч. IV, раздел 30.5). Числен-ное решение показано на рис. 30.8, где для конкретности мы положилип = 1.52,b = 0.9(7. Левый рисунок представляет собой коэффициент про-хождения для одного, двух и четырех барьеров, правый --- для десятибарьеров. Последний случай, когда число барьеров велико (N 
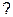1)представляет для нас особый интерес. Тенденции, обнаруживающиесядля N = 10, в пределе N> 
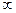станут только отчетливее. А именно: сростом N некоторые минимумы становятся глубже и шире, и в пределезначение коэффициента прохождения в них стремится к нулю. Наоборот,амплитуда колебаний 
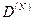при других частотах становится меньше и
коэффициент прохождения стремится к единице. Физическое объяснениеэтого явления заключается в том, что выполнении определенных условийотраженные от концов прямоугольных барьеров волны взаимно компен-сируют, гасят друг друга.
Подчеркнем еще раз: для предельного случая периодической струк-туры (N> 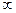) зависимость коэффициента прохождения 
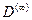от частоты
падающего света такова, что
30.8. Оптическая аналогия прохождения частицы над барьером
157
а
к
X
ф
О
X
О
О.
П.
\ -
X
ф
-8-
-8-
о
О
Рис. 30.8: Коэффициент прохождения в зависимости от частоты падающего света для малого (слева) и большого (справа) числа барьеров. Видна тенденция формированияпри N> 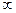широких минимумов (т.н. запрещенныхзон,непрозрачных для света иличастицы) и максимумов с D>1(т.н. разрешенных,абсолютно прозрачных зон).
• имеются целые полосы частот, в которых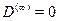 
; для таких ча-стот составной барьер непрозрачен, свет этих частот полностью от-ражается от структуры.
• для других же частот, наоборот,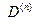 
= 1, т.е. для них барьер пол-
ностью прозрачен, не происходит никакого отражения, свет свободно
распространяется в такой структуре (на этом явлении основано со-здание т.н. просветленных объективов).
Аналогичное явление происходит и для квантовомеханической частицы,распространяющейся в периодическом потенциальном поле. При некото-рых значениях энергии частицы бесконечная периодическая последова-тельность потенциальных барьеров становится для нее совершенно не-прозрачной, даже если энергия частицы превышает высоту барьера. Придругих энергиях, наоборот, периодическая потенциальная структура ста-новится для частицы абсолютно прозрачной. Так возникают запрещен-ные и разрешенные энергетические зоны в кристалле, и мы с ними в своевремя познакомимся поближе.
Контрольные вопросы
• В чем заключается вероятностная интерпретация волновой функции?
Глава 30. Уравнение Шредингера
• Что такое условие нормировки волновой функции и в чем его физический смысл?
• Запишите общее уравнение Шредингера. Какому соотношению классической фи-зики оно соответствует?
• Как действует на волновую функцию оператор импульса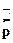 
?
• Как действует на волновую функцию оператор координаты г и любая функцияэтого оператора f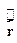
?
• Что такое гамильтониан системы?
• Запишите стационарное уравнение Шредингера.
• При решении стационарного уравнения Шредингера для некоторой системы полу-чается ряд значений энергии: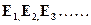 
. .. Может ли экспериментатор получить
какое-то иное значение при измерении энергии этой системы?
• Что такое вырождение энергетических уровней?
• Дайте наглядное объяснение, почему квантуется энергия частицы, находящейся вбесконечно глубокой потенциальной яме.
• Что такое нулевые колебания квантового осциллятора? Почему их существованиенеизбежно?
• * Сформулируйте принцип соответствия Н. Бора.
• В бесконечно глубокой потенциальной яме расстояние между высоколежащими
уровнями возрастает с ростом номера уровня п (см. (30.24)). В то же время, ка-залось бы, принцип соответствия Бора требует, чтобы уровни сгущались к клас-сическому значению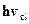
. Покажите, что принцип соответствия справедлив и для
этой системы.
• Пусть частица налетает на потенциальный барьер, причем ее энергия большевысоты барьера: Е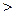 
U.Можно ли по результату такого процесса обнаружитьразницу между предсказаниями классической и квантовой теорий?
• Что такое эффект туннелирования? Почему он не наблюдается в нашей повсе-дневной жизни?
• Металлическая шайба массой т = 10 г скользит по гладкой поверхности соскоростью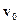 
= 1м/с. На ее пути стоит небольшая горка с гладкими скло-нами. Высота горки Н = 5.5 см, ее ширина d = 10 см. Как известно из курсамеханики, начальная скорость шайбы позволяет ей подняться лишь на высоту
= 
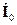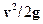= 1/(2 X 9.8) = 5.1 10-2 м = 5.1 см. Квантовая же механика утвер-ждает, что в принципе шайба может оказаться по другую сторону горки. Оценитьвероятность такого события.
• Квантовая механика дает только вероятностное описание движения частиц, гово-рить об их положении, скорости и т.п. смысла не имеет. Как Вы думаете, кактогда эта теория может широко использоваться при проектировании, например,устройств, использующих квантовые свойства систем?
Глава 31
Теория атома
Раз уж мы получили в руки такое мощное оружие, как уравнение Шре-дингера, то естественно вернуться к атому, начав с простейшего ---- атома водорода. Надо же убедиться, что квантовая механика при-ведет к тем же результатам, что и полуклассическая теория атома поБору. К тому же есть надежда, что новая теория подарит нам неожи-данные открытия. Жаль только, что изучение способов решения урав-нения Шредингера не входит в рамки настоящего курса. Но не беда:мы постараемся обойтись без излишней математики, угадывая свойстварешений на основе интуиции, выработанной при изучении классическойфизики. Следует только помнить, что читателя никто обманывать несобирается: все ``угаданное" может быть получено из уравнения Шре-
дингера точными математическими расчетами.
Дата добавления: 2016-01-26; просмотров: 952;