Задача 31.27. Найти электростатический потенциал, создаваемый ато-мом водорода в основном состоянии.

Решение. Возьмем любую точку на расстоянии R от ядра. Электро-статический потенциал в ней создается, во-первых, положительным за-рядом е ядра и, во-вторых, той частью заряда электрона, которая на-ходится внутри сферы радиусом R. Хорошо известно, что сфериче-ски симметричное распределение заряда не создает поля во внутреннихобластях. Поэтому часть электронного облачка, находящаяся дальшевыбранной точки, не внесет вклада в потенциал. Поскольку в уравне-нии вычислена вероятность W(R) нахождения электрона внутрисферы радиусом R, то отрицательный заряд внутри этой сферы равен

Глава 31. Теория атома

--- еW(R). Поэтому потенциал в точке R, создаваемый эффективным за-рядом q(R) = е(1 --- W(R)), имеет вид:

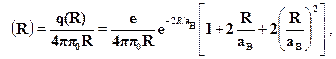
На больших расстояниях потенциал убывает экспоненциально,то есть гораздо быстрее обычного кулоновского потенциала точечногозаряда. Это --- так называемый эффект экранировки: отрицательныйзаряд электрона компенсирует положительный заряд ядра. При R >0 потенциал переходит в обычный кулоновский потенциал: мыпроникли внутрь электронного облачка, где оно уже не экранирует зарядядра. ¦

Для энергии из уравнения Шредингера получается в точности такаяже формула, что и из теории Бора:

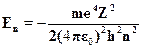
Как видно, энергия действительно не зависит от квантовых чисел /,т.При этом, как следует из свойств решений уравнения , азимуталь-ное квантовое число l принимает целые значения от 0 до n --- 1. И этосвойство, угаданное нами на основе классической физики, воспроизвелосьв квантовой механике.

Удивительно, как квантовая механика, низвергнувшая столько клас-сических представлений, дает аналогичные результаты там, где вдело вступают свойства симметрии системы. Отсюда вывод: сим-метрия играет более важную роль, чем конкретные физические за-коны. Когда нибудь будут открыты новые законы, которые обобщати квантовую механику, и все теории, которые ныне находятся на пе-реднем крае науки. Но свойства симметрии системы проявят себятак или иначе.

Отличие квантовой механики от теории Бора --- более богатая структурауровней: состояние определяется тремя квантовыми числами, как и втрехмерном потенциальном ящике. Кстати, это не случайно. Три кван-товых числа в потенциальной яме и в атоме водорода --- отражение трех-мерности нашего пространства. Подсчитаем кратность вырождения, тоесть число различных состояний с той же энергией (главным квантовым

31.3. Атом водорода

171

числом п). При данном п число l пробегает значения от 0 до п--- 1 икаждому из них соответствует 2l + 1 значение m. Поэтому кратностьвырождения N равна

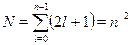
При п = 1 имеем N = 1, то есть основной уровень не вырожден. Прип = 2 кратность вырождения равна 4: уровень с l = 0 и три уровня сl = 1 и различными проекциями момента импульса т = ---1,0,+1. Прип = 3 кратность вырождения N = 9: один уровень с l = 0, три уровняс l = 1 и пять уровней (по числу проекций) с l = 2. Для классификацииуровней энергии по значению квантового числа l применяют условныеобозначения, позаимствованные из спектроскопии, где они появились ещедо создания теории атома:

l= 0 1 2 3 4 5 ...

символ s р dfg h...

Главное квантовое число ставится впереди символа. Примеры возмож-ных состояний:

1s, 2s, 2р, 3s, 3р, 3d, 4s, 4р, 4d, 4f еtс.

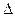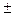При переходе электрона с уровня на уровень излучается фотон, унося-щий собственный угловой момент, равный h. Следовательно, разрешенытолько переходы с изменением l на единицу: возникает правило от-бора l = 1. Это значит, что в атоме водорода допустимы переходыпр >1s, пs > 2р, еtс, приводящие к тем же спектральным сериям, чтои теория Бора. Более богатая структура уровней не проявляется пока вбольшем разнообразии атомных спектров из-за вырождения.

Говоря о вырождении уровней, мы имели в виду водородоподобныйатом. В более сложных атомах или в присутствии внешних электро-магнитных полей вырождение, как говорят, снимается и появляется за-висимость энергии от чисел l,т. Любая не кулоновская центрально-симметричная поправка к потенциальной энергии приведет к зависимо-сти уровней энергии от l (наблюдается в щелочных металлах). В клас-сической физике такая поправка к обычному закону притяжения (напри-мер, планеты к Солнцу) превращает эллиптические орбиты в незамкну-тые кривые. Обращаясь по таким орбитам, планета как-бы движетсяпо обычному эллипсу, который дополнительно вращается как целое, пре-цессирует в той же плоскости. Подобный эффект --- вращение перигелия

Глава 31. Теория атома

Меркурия, предсказала общая теория относительности. Новое движениеприводит к дополнительный энергии вращения, зависящей от l. В ре-зультате энергия уровня 2s перестанет совпадать с энергией уровня 2ри т.п.

Любое не центрально-симметричное поле (например, магнитное) сни-мет вырождение по ш. В классической физике магнитное поле вызываетпрецессию плоскости вращения вокруг направления поля и также по-явление из-за этого вращения дополнительной энергии. Сказанное можносформулировать в виде общего вывода:

Всякое дополнительное взаимодействие, нарушающее симметрию си-стемы, снимает соответствующее ей вырождение уровней энергии.На эксперименте снятие вырождения проявляет себя в расщеплениипрежних спектральных линий на несколько компонентов.

• Спин электрона и тонкая структура спектров

Дальнейшее исследование атомных спектров показало, что многие спек-тральные линии имеют два близких компонента. Так, еще в 1887 г.А. Майкельсон обнаружил расщепление ---линии серии Бальмера в водо-роде (порождаемой переходом 3р > 2s): она оказалась состоящей из двух

линий со средней длиной волны 6563 Е и разностью длин волн 0.14 Е (т.е.относительная величина расщепления порядка 10-5). Были обнаруженыи линии, расщепленные на 3, 4 и более компонентов. Расщепление линий,как мы теперь понимаем, означает расщепление энергетических уровнейатома: у них появляется, как говорят, тонкая структура. Значит, су-ществует неучтенное взаимодействие. Мы говорили, что расщеплениелиний появляется, например, когда наложенное внешнее поле нарушаетсимметрию системы. А здесь неучтенное взаимодействие проявляется вотсутствии внешних полей, то есть оно должно быть связано с какими-товнутренними свойствами атома.

Оказалось, что здесь действительно проявились внутренние свойства,но не атома в целом, а электрона. В 1925 г. С. Гаудсмит и Дж. Улен-бек выдвинули гипотезу спина электрона: они предположили существо-вание у электрона собственного момента импульса, не связанного с ор-битальным движением. Сначала спин представляли себе как верчение(англ, spin) электрона вокруг собственной оси (аналог суточного враще-ния Земли). Потом осознали, что ``верчение'' нельзя понимать буквально:

31.4. Спин электрона и тонкая структура спектров

173

численные оценки давали линейную скорость верчения, превышающуюскорость света.

• Сейчас под спином понимается собственный момент количества дви-жения электрона как врожденное квантовое свойство. Его существо-вание остается загадкой, если находиться только в рамках квантовоймеханики Гейзенберга-Шредингера. Естественное объяснение спинполучил только в релятивистской квантовой теории Дирака, соеди-нившей теорию относительности с квантовой механикой.

Из опытов следовало, что электрону надо приписать спиновое квантовоечисло s = 1/2, имеющее те же свойства, что и квантовое число /: соб-ственные значения оператора квадрата спина равны h2s(s + 1) = 3h2/4, апроекция спина на какую-то ось пробегает через единицу все значения отмаксимального до минимального (для электрона проекция спина sz = 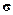/h,где а принимает лишь значения 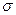= 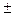1/2).

Откуда же взялось расщепление спектральных линий? Попытаемсяпонять это с помощью полуклассических рассуждений. В классическойфизике любое вращение электрического заряда создает магнитное поле.Вращающийся по орбите классический электрон можно представить каквиток с током силой I, охватывающий площадь S, т.е. как диполь смагнитным моментом 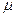=IS (эту формулу знал еще Ш. Кулон). Клас-сическая оценка: электрон на орбите радиусом R и скоростью 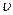имеетпериод обращения 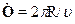. Возьмем какую-нибудь точку на орбите.За время Т через нее проходит заряд е, то есть сила тока по определе-нию равна I = е/Т = е 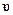/2 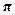R. Кроме того, электрон имеет орбитальныймомент L=тe 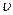R, так что ток можно выразить через орбитальный мо-мент, исключив скорость электрона: I=еL/(2тет 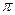R2) = еL/(2теS), гдемы ввели площадь ``витка'' S= 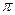R2. Тогда орбитальный магнитныймомент, создаваемый электроном, равен 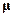= еL/2mе. Заменим теперь всоответствии с правилами квантования 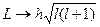и получим выра-жение для орбитального магнитного момента, которое может быть вы-ведено и более строго:

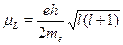
Отсюда следуют выводы:

• Естественная единица для магнитных моментов в микромире --- так

Глава 31. Теория атома

называемый магнетон Бора

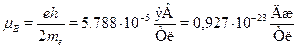
• Проекция магнитного момента на любую ось всегда должна быть це-лым кратным магнетона Бора: 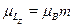. Теперь понятно, почему

квантовое число m названо магнитным.

• Отношение магнитного момента к орбитальному моменту количе-ства движения равно е/2mе (его называют гиромагнитным отноше-нием) .

Эксперименты показали, что электрон обладает двойным магнетиз-мом: его собственный магнитный момент, связанный со спином, равен 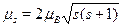, то есть гиромагнитное отношение для него оказалосьв два раза большим (е/те). Это --- лишнее доказательство, что электроннельзя представлять себе как заряженный шарик, вращающийся вокругсобственной оси: в таком случае должно было бы получиться обычноегиромагнитное отношение. Для проекции собственного магнитного мо-мента имеем 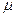sz = 2 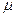B 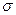и поскольку 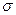= 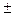1/2, то 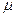sz = 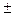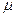B. В итогедля проекции спинового магнитного момента снова получились целыекратные магнетона Бора как и для орбитального движения. По какой-топричине природа предпочитает иметь дело с целым магнетоном Бора,а не с его частями. Поэтому полуцелое значение собственного моментаколичества движения она компенсирует двойным гиромагнитным отно-шением.

Теперь можно понять, почему наличие у электрона собственного маг-нитного момента приводит к появлению какого-то неучтенного до сих порвзаимодействия. Для этого опять перейдем на полуклассический язык.Орбитальное движение электрона создает магнитное поле, которое дей-ствует на собственный магнитный момент электрона. Подобным образоммагнитное поле Земли воздействует на стрелку компаса. Энергия этоговзаимодействия сдвигает энергетические уровни атома, причем величинасдвига зависит, вообще говоря, от спинового и орбитального моментовколичества движения.

Взаимодействие спинового и орбитального магнитных моментов при-водит к снятию вырождения и к расщеплению спектральных линий.

31.4. Спин электрона и тонкая структура спектров

175

Задача 31.28.Оценить расщепление уровней энергии вследствие взаи-модействия спинового и орбитального магнитного моментов электрона ватоме водорода.

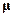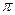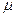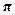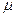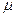Решение.Круговой виток радиусом R с током силой I порождает вцентре магнитное поле В= 0I/2R. В этой главе было показано, чтовращающийся по орбите электрон можно представить как виток с токомI=еL/(2 mR2) ? B/( R2). Здесь для оценки мы положили L? h.Тогда получаем для магнитного поля, создаваемого орбитальным дви-жением электрона в атоме величину порядка В? 0 B/(2 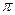R3). Энергиявзаимодействия собственного магнитного момента электрона с этим маг-нитным полем равна по порядку величины:

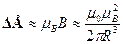
Для оценки положим R равным боровскому радиусу первой орбиты ощ.Подставляя сюда выражения для аВ и В и учитывая, что 0 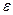0 = 1/с2,получаем оценку сдвига энергетических уровней:

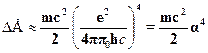
где 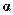--- введенная выше постоянная тонкой структуры. Энергия первогоуровня атома водорода, как известно, равна Е = 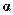2тс2 /2, так что можно переписать как 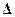Е ? 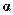2Е. Поскольку 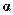? 1/137, а Е = 13.6 эВ,то 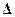Е ? 0.72 мэВ, а относительный сдвиг уровней 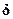Е = 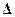Е /Е ? 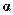2 ? 5 10-5, что соответствует экспериментальным данным. ¦

Это есть оценка (не расчет) искомого расщепления уровней. В сущ-ности, расщепление уровней --- это релятивистский эффект: по Борускорость электрона на первой орбите ? с и Е ? ( /с)2. Поэтомуне удивительно, что до конца свойства спина могут быть поняты тольков релятивистской квантовой теории. Мы не ставим себе такую задачу,но просто будем учитывать наличие у электрона этого удивительногосвойства.

Прямое экспериментальное доказательство существования спина элек-трона было дано в опыте Штерна-Герлаха в 1922 г. Идея опыта состоитв том, что в магнитном поле, неоднородном по оси z, на электроны дей-ствует смещающая сила, направленная вдоль поля.