Происхождение этой силы проще уяснить сначала на примере элек-трического диполя, помещенного в электрическое поле. Электрический

Глава 31. Теория атома

диполь представляет собой пару противоположных зарядов 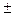е, располо-женных на малом расстоянии l друг от друга. Величина электрического

момента определяется как 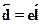, причем вектор 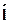считается направлен-ным от отрицательного заряда к положительному.

Пусть положительный заряд находится в точке , а отрицательный ---в точке , так что 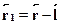. Пусть диполь помещен в электрическоеполе с напряженностью 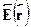. Найдем силу, действующую на диполь. Наположительный заряд действует сила 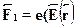, на отрицательный --- 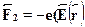. Результирующая сила

Так как расстояние между зарядами мало, то поле в точке расположенияотрицательного заряда можно приближенно записать как

Подставляя это разложение в выражение для силы Е, находим

.

Если поле однородно ( не зависит от ), то на заряды диполя действуютравные и противоположно направленные силы и результирующая силаравна нулю, как и следует из уравнения . Как известно, такаяпара сил не смещает диполь (который в целом электрически нейтрален),но лишь поворачивает его вдоль поля (магнитный аналог --- стрелкакомпаса). В неоднородном же поле результирующая сила отлична отнуля. В частном случае, когда поле зависит только от координаты 2,в уравнении отлична от нуля лишь производная по 2:

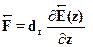
где dz --- проекция электрического момента на ось z. Неоднородное полестремится втянуть диполь в область, где оно сильнее.

Магнитных зарядов не существует, но магнитный диполь реализуетсявитком с током и его свойства аналогичны свойствам электрическогодиполя. Поэтому в формуле надо заменить электрическое полена магнитное, электрический момент --- на магнитный и написать длясилы, действующей на электрон в опыте Штерна-Герлаха, аналогичноевыражение:

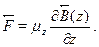
31.4. Спин электрона и тонкая структура спектров

177

Схема опыта: пучок атомов пролетает сквозь неоднородное магнит-ное поле, направленное поперечно к скорости атомов. Сила, действую-щая на магнитные моменты атомов, отклоняет их. Соответственно воз-можным значениям проекции магнитного момента на направление поля,первоначальный пучок расщепляется на несколько пучков. Если пол-ный магнитный момент атома определяется только спином электрона, топервоначальный пучок расщепится на два. Для многоэлектронных ато-мов расщепленных пучков может быть больше. Для своего экспериментаШтерн и Герлах использовали серебро, которое испарялось в электриче-ской печке. Численные значения расщепления составляли доли миллиме-тра. Авторы подчеркнули в своих выводах, что неотклоненных атомов небыло зарегистрировано. Ниже мы увидим, что это --- специфика опытовс элементами первой группы.

Главный результат опытов Штерна и Герлаха --- прямое эксперимен-тальное доказательство квантования направления магнитного моментаатомов. Согласно классической физике, первоначальный пучок должен нерасщепиться, а размазаться в соответствии с произвольностью проекциимагнитного момента на направление магнитного поля. Соответственно,на экране за прибором вместо двух раздельных линий, оставленных ато-мами серебра, должна была бы наблюдаться размытая полоска.

Задача 31.29.Узкий пучок атомов со скоростью 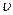и массой т пропус-кается через поперечное неоднородное магнитное поле, в котором на нихдействует сила Fz (рис. 31.3). Протяженность поля l1, расстояние от маг-нита до экрана l2. Определить отклонение следа пучка атомов на экранеот его положения при выключенном магнитном поле.

Решение.Здесь мы имеем дело с задачей классической механики, ко-торая позволяет подготовиться к количественному рассмотрению опытаШтерна-Герлаха. Время пролета атома через магнит равно t = l1/ 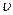.Все это время на атом действует поперечная сила ЕД придающая емупоперечное ускорение а=Fz/т. За время пролета атом отклонится нарасстояние s1 = аt2/2=Fz 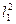/(2т 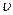2) и приобретет поперечную скорость . Это значит, что из магнита атом вылетает подуглом 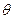к первоначальному направлению движения, причем tg 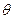= 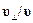.Следовательно, при пролете расстояния l2 до экрана атом отклонитсяеще и на расстояние 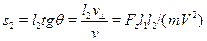. Складывая

Глава 31. Теория атома

Рис. 31.3: К задаче (31.29.) об отклонении атомов магнитным полем: ОА= s1,АВ=

s2, ОВ = s.

отклонения s1 и s2, получаем искомое отклонение следа атома на экране:

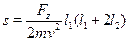
Часто в задаче стоит вопрос об отклонении пучка атомов при выходе измагнита. В таком случае надо положить l2= 0 в полученной формуле. ¦

Задача 31.30.Узкий пучок атомов серебра при прохождении магнит-ного поля с неоднородностью дВ/дz = 1 кТл/м протяженностью l1 =4 см расщепился на два пучка. Экран для наблюдения установлен нарасстоянии l2 = 10 см, скорость атомов 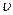= 0.5 км/с. Определить рас-стояние b между компонентами расщепленного пучка на экране.

Решение.Заполненные оболочки дают нулевой вклад в магнитный мо-мент атома. Атом серебра имеет один валентный электрон, и потомуего магнитный момент равен магнитному моменту электрона. В неод-нородном поле на атом действует сила 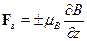где 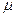B --- магнетон

Бора. Знаки 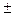соответствуют двум возможным направлениям магнит-ного момента электрона и потому пучок расщепляется на два. На экраненаблюдаются две полоски, находящиеся на расстоянии b друг от друга.Если в формулу подставить выражение для силы Fz, то получимдва отклонения s, отличающиеся знаком. Поэтому искомое расщеплениеb = 2s. В результате приходим к выражению:

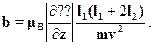
Массу атома серебра легко найти по таблице Менделеева: молярнаямасса атомная масса М = 107.868 г/моль. Чтобы найти массу, надо

31.5. Векторная модель атома

М разделить на число Авогадро: т = 107.868 10-3/6.02 10-23 = 1.7910-25 кг. Подставим теперь в численные значения:

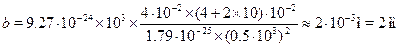
Такое расщепление вполне наблюдаемо в опытах.

• Векторная модель атома

Обсудим качественные изменения, вносимые спином электрона в теориюатома. Полный момент импульса складывается теперь из орбитальной 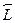и спиновой 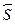частей. Возникает новое квантовое число j принимаю-щее два значения 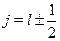(при l = 0 полный момент импульса j = 1/2).Эти значения соответствуют двум случаям, когда спин параллелен и ан-типараллелен орбитальному моменту импульса. Необходимо ввести но-вые обозначения уровней: добавляется индекс, указывающий величинуполного момента импульса: уровни обозначают пxj где п --- главноеквантовое число, a x --- прежний буквенный символ для обозначения ве-личины азимутального квантового числа l. Свойства полного моментате же, что и у орбитального и спинового моментов. Как следствие но-вого вида взаимодействия возникает более богатая структура атомныхспектров, наблюдавшаяся на опыте. Проиллюстрируем это на примерепервых возбужденных уровней атома водорода (таблица 31.1).

Энергия уровней уже выражается не формулой Бора, но содержит по-правки относительной величины 2. Мы не станем ее приводить, ноотметим характерное свойство: в отсутствие внешних полей энергия по-прежнему не зависит от орбитального момента l, но лишь от полногомомента импульса j. Значит, уровни 2s1/2 и 2р1/2 вырождены (их энер-гии совпадают). Уровень 2р3/2, как оказывается, лежит чуть выше.

Состояния многоэлектронных атомов классифицируются подобным обра-зом. Если 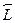--- суммарный орбитальный момент всех электронов, а 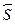---их суммарный спиновый момент, то полный момент системы определя-ется как 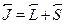. Соответственно и обозначается это состояние как2S+1XJ. Под X понимается тот же буквенный символ, обозначающий зна-чение орбитального момента количества движения (только в этом слу-чае используется заглавная буква). Верхний левый индекс равен числуспиновых состояний (для одиночного электрона в нем не было необходи-мости, так как его спин всегда равен 1/2).

Глава 31. Теория атома

Таблица 31.1: Схема нижних уровней атома водорода

Итак, пусть дано состояние 2S+1XJ. Встает вопрос: чему равен маг-нитный момент системы 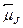? Ясно, что он направлен вдоль полного мо-мента количества движения , а его размерность определяется магнето-ном Бора 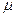B- Тогда

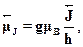
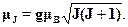
Для гиромагнитного отношения (обобщение аналогичной величины, свя-занной с орбитальным и спиновым моментами) можно тогда написатьвыражение вида еg/2те. Коэффициент пропорциональности g называ-ется множителем Ланде или просто (g-фактором. Для орбитального дви-жения g = 1, для спинового магнитного момента g = 2. Задача о магнит-ном моменте атома сводится к нахождению зависимости g от квантовыхчисел J, L и S.

Ответ можно получить с помощью простой полуклассической модели,получившей название векторной модели атома. Сначала возведем в ква-драт уравнение, связывающее 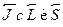: 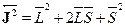. Квадратымоментов можно выразить через соответствующие квантовые числа поуже известным нам правилам. Находим тогда выражение для скалярного

31.5. Векторная модель атома

произведения

Полный магнитный момент складывается из магнитного момента, со-здаваемого суммарным орбитальным моментом количества движения,и суммарного спинового магнитного момента. Но спин, как уже гово-рилось, обладает двойным магнетизмом. Поэтому с учетом уравнения можно записать:

Сокращая общий множитель 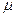B и умножая обе части на , в правойчасти заменен на ), получаем:

Если подставить сюда выражение для скалярного произведения , то получим окончательный ответ:

Убедимся, что эта формула воспроизводит уже известные результаты.Если полный спиновый момент равен нулю, то полный момент совпа-дает с орбитальным. Подставляя в значения S = 0, J = L,получаем g = 1, как и должно быть для магнитного момента, создава-емого чисто орбитальным движением электронов. В обратном случаенулю равен орбитальный момент и полный момент количества движе-ния равен спиновому. Подставляя в значения L = 0, J = S, на-ходим g = 2 в полном согласии с двойным магнетизмом спинового мо-мента. Именно такой случай реализуется для элементов первой группы вопыте Штерна-Еерлаха. Упоминалось, что для сложных атомов (напри-мер, серы) расщепление пучков будет более сложным. Теперь мы можемпредсказать результат количественно. Основное состояние серы 3Р2, тоесть S=1, L=1, J = 2. Из формулы для множителя Ланделегко получаем g = 3/2, так что магнитный момент атома равен

Глава 31. Теория атома

Проекция магнитного момента на ось z

где тJ (проекция полного момента количества движения) принимаетпять различных значений в соответствии с правилами квантования мо-мента: тJ = 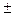2, 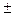1, 0. Теперь, используя результаты задач в концеглавы, можно рассчитать расщепление пучка атомов серы в опыте Штерна-Герлаха. Ясно, что пучок расщепится на пять компонентов, причем однаиз них (тJ = 0) не будет отклоняться магнитным полем.

• Принцип Паули и валентность элементов

Мы видели, что орбитальный момент импульса характеризуется азиму-тальным квантовым числом l, принимающим целые значения. Собствен-ный спиновый момент характеризуется спиновым квантовым числом s,равным 1/2 для электрона. Спин --- фундаментальное квантовое свой-ство всех элементарных частиц. В соответствии со значением спиновогоквантового числа 5 частицы делятся на два класса: бозоны (целые s) ифермионы (полуцелые s). Другие значения s науке не известны. При-меры фермионов: электрон, мюон, нейтрино, кварки, частицы из трехкварков (протон, нейтрон). Пример бозонов: фотон, недавно открытыеW 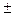и Z частицы из двух кварков ( 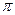-мезоны и др.).

• Бозоны и фермионы --- это не имена собственные каких-то частиц,а названия целых семейств. Каждая микрочастица принадлежитодному из них и поменять принадлежность уже не в состоянии. Втеории элементарных частиц замечено, что из фермионов построеновещество, а бозоны переносят фундаментальные взаимодействия.

Если собрать вместе несколько бозонов, то они не мешают друг другузанять низшее энергетическое состояние и, следовательно, все там ока-жутся. Поведение коллектива фермионов регулируется принципом Па-ули:

• два одинаковых фермиона не могут находиться в одном и том жесостоянии.

В применении к атому принцип Паули запрещает двум электронам иметьодинаковый набор квантовых чисел: состояния электронов должны от-личаться значением хотя бы одного из них. Если бы принципа Паули

31.6. Принцип Паули и валентность элементов

183

не существовало, то у всех атомов в основном состоянии все электронынаходились бы на нижнем энергетическом уровне и атомы различныхэлементов были бы до ужаса похожи друг на друга. Таким образом,известная нам химия, все разнообразие элементов и их свойств (в част-ности, гамма вкусовых ощущений, отличающая, скажем, вино от сыра)--- следствия принципа Паули. До сих пор мы в основном рассматривалитолько атом с одним электроном. Станем добавлять лишний электрон и,соответственно, увеличивать на единицу заряд ядра. Иными словами, со-вершим прогулку по таблице Менделеева. Введем понятия оболочки каксовокупности уровней с одинаковыми главными квантовыми числами п иподоболочки (уровни данной оболочки с одинаковыми l). Традиционныеобозначения

п = 1, 2, 3, 4, ...

символ К, L, М, N ....

Число уровней в оболочке мы фактически уже подсчитали: оно равнократности вырождения по т и /, умноженной на 2 в соответствии с двумявозможными направлениями спина электрона. Таким образом, оболочкаможет вместить 2п2 электронов, а подоболочка --- 2(2l + 1) электронов(число различных значений m, удвоенное по той же причине). Состоя-ния в атоме различаются квантовыми числами п, l, т и 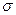(проекцияспина). По принципу Паули лишь один электрон может иметь данныйконкретный набор квантовых чисел.

Напоминание: три квантовых числа п, l и т отражают трехмер-ность пространства, 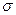--- внутренние свойства электрона.

Порядок замещения уровней в многоэлектронных атомах определяетсяэнергией уровней с учетом влияния заполненных оболочек. Нижние обо-лочки частично экранируют заряд ядра, что ведет к некулоновскомуполю для высших оболочек. Этим объясняется зависимость энергииуровней от квантового числа l. Чем больше l, тем дальше находитсяэлектрон от ядра и тем слабее его связь с ядром, т.е. такой уровеньлежит выше. При больших моментах (состояния d, f и т.п.) уровеньблизок или даже выше s-подуровней следующей оболочки. В целом за-полнение идет в таком порядке (случаются небольшие отклонения):

1s | | 2s, 2р | | 3s, 3р | | 4s, 3d, 4р | | 5s, 4d, 5р | | 6s, 4f, 5d, 6р | | еtс.

В этом ряду знаком | | отделены периоды таблицы Менделеева. В соот-ветствии с полученными формулами для числа уровней в зависимости от

Глава 31. Теория атома

п и /, / период содержит 2 элемента, II и III --- по 8, в IVиV --- по 18элементов. Здесь ``вклиниваются'' заполнения d-подоболочек (по 10 эле-ментов --- переходные металлы). В VI периоде добавляется заполнение/-подоболочки (14 элементов --- лантаниды) и т.д.

Химические свойства зависят в основном от строения внешней элек-тронной оболочки (валентных электронов). Отсюда и вытекает перио-дичность повторения свойств элементов. Так, у благородных газов за-полнены внешние 5--- и р---подоболочки из 8 электронов. У элементов пер-вой группы (щелочные металлы) на внешней оболочке имеется всего одинэлектрон, а галогенам (VII группа) не хватает одного электрона для за-полнения внешней р---подоболочки. Все эти рассуждения хорошо знакомыпо курсу химии, но они носят качественный характер. Как известно,валентность элемента определяется не столько количеством электронов,сколько степенью легкости, с которой их можно вырвать из атома. По-нятно, что внешние электроны оторвать легче, но хотелось бы получитьхоть какой-нибудь количественный критерий. Таким критерием можетслужить так называемый потенциал ионизации --- энергия, которую не-обходимо затратить, чтобы удалить электрон из атома. Расчет сложныхатомов непрост, но в целом таблица Менделеева объясняется квантовоймеханикой. Мы ограничимся лишь самыми простыми атомами и точ-ные расчеты заменим количественными оценками. Экспериментальныерезультаты представлены на рис. 31.4.