Электронная конфигурация атомов

Для атома любого элемента мы можем указать его электронную кон-фигурацию. Теперь познакомимся с двумя правилами, позволяющимиузнать для основного состояния каждого атома значение его суммарныхмоментов: спинового S, орбитального L и полного J.

• Наименьшей энергией обладает атом с наибольшим возможным приданной электронной конфигурации значением 5 и наибольшим воз-можным при этом S значением L(правило Хунда).

• Если в незаполненной подоболочке атома находится не более поло-вины максимально возможного для нее числа электронов, то J =| L --- S| . Если же подоболочка заполнена более, чем наполовину, то

J=L + S.

Правило Хунда является эмпирическим (т.е. не выведенным из теории,а установленным экспериментально); второе правило выводится из него

Глава 31. Теория атома

и из полученной выше формулы для скалярного произведения 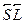.Для облегчения применения правила Хунда полезно запомнить, что:

1) надо рассматривать только незаполненную электронную подоболочку,так как моменты электронов в заполненных подоболочках взаимнокомпенсируются;

2) значения S и L одинаковы для двух подоболочек, из которых однаимеет столько электронов, сколько не хватает для заполнения дру-гой.

Для примера применения указанных правил рассмотрим атом серы. Егоатомный номер Z = 16 и, следовательно, электронная конфигурацияимеет вид 1s22s22рб3s23р4:. Индексы справа вверху обозначают числаэлектронов в указанных состояниях. Видим, что незаполненной остаетсятретья оболочка, на которой находятся четыре электрона с орбиталь-ными моментами, равными единице. При данном L = 1 согласно прин-ципу Паули параллельными могут быть лишь спины трех электронов,отличающихся значениями m = ---1,0,1. Спин четвертого электронадолжен быть направлен в противоположную сторону, и потому макси-мально возможное значение суммарного спина для данной конфигурацииравно S= 3/2 --- 1/2 = 1.

При этом значении 5 сумма проекций орбитальных моментов элек-тронов с одинаково направленными спинами равна нулю, следовательно,максимально возможное значение проекции суммарного орбитального мо-мента определяется четвертым электроном и равна единице. ПоэтомуL = 1. Так как внешняя подоболочка заполнена более чем наполовину,то J = L+S = 2. Мы пришли к выводу, что основным состоянием атомасеры является 3Р2.

Для сравнения найдем основное состояние атома кремния (Z = 14).От атома серы он отличается тем, что на внешней подоболочке у негонаходятся два, а не четыре р-электрона. Для ее заполнения не хватает че-тырех электронов, то есть столько, сколько их имеется у серы. Поэтомудля атома кремния получаем те же значения S = 1 и L = 1. Внешняяподоболочка заполнена менее чем наполовину, откуда J = | L --- S| = 0.Поэтому основным состоянием кремния является 3Р0.

31.6. Принцип Паули и валентность элементов

189

Контрольные вопросы

• Сформулируйте правила квантования момента импульса и проекции момента навыделенную ось.

• Какими квантовыми числами описывается состояние электрона в атоме? От какихквантовых чисел зависит энергия электрона?

• Какова кратность вырождения энергетического уровня в атоме водорода?

• Какова размерность волновой функции электрона в СИ?

• Чему равен потенциал ионизации атома водорода? Какова зависимость энергииэлектрона от главного квантового числа?

• В каких аспектах волновая теория атома совпадает с теорией Бора, а в каких этитеории различны?

• Перечислите свойства электрона, связанные с наличием у него спина.

• Что такое магнетон Бора? Чему равно гиромагнитное отношение для орбиталь-ного движения и для спина?

• Опишите схему опыта Штерна-Герлаха. От чего зависит число компонентов, накоторые расщепляется пучок атомов в этом опыте?

• Почему направление магнитного момента электрона противоположно направле-нию его спина?

• Сформулируйте принцип Паули. Что такое электронные оболочки и подоболочкив атоме? Объясните роль принципа Паули в повторяемости (периодичности)свойств химических элементов.

• Как связан потенциал ионизации с валентностью элемента? Почему электронтруднее удалить из атома неона, чем из атома натрия?

• Предположим, что никакого спина у электрона не существует, так что его со-стояние в атоме определяется лишь тремя квантовыми числами п,1,т. Какиепоследствия это имело бы для таблицы элементов Менделеева и нашей жизни?

• Предположим, что спин электрона равен 3/2. Какой элемент играл бы тогда рольгелия --- первого из группы благородных газов? Какой элемент был бы вторым вэтой же группе?

• * Найти основное состояние атома фосфора (Z = 15).

Глава 32

Физическая природа химическойсвязи

32.1 Молекулы

Атомы представляют собой связанные электрическими силами системыядер и электронов. В свою очередь, атомы под действием тех же силв определенных условиях могут объединяться в молекулы. Первона-чально химия предполагала существование специфических ``химическихсил'' для объяснения образования молекул из атомов, а также химиче-ских реакций между атомами или молекулами. Однако таких ``химиче-ских сил'' не существует: образование молекул обусловлено обычнымиэлектрическими (кулоновскими) силами взаимодействия между заряжен-ными частицами, т.е. электронами и ядрами, из которых состоят атомы.Но механизм образования молекул можно понять только на основе кван-товой механики. Для простоты ограничимся рассмотрением простей-ших двухатомных молекул. Силы, удерживающие атомы в молекуле,вызваны взаимодействием внешних электронов, а электроны внутреннихоболочек при объединении атомов в молекулы остаются в прежних состо-яниях. Различают два вида связи между атомами в молекуле: ионную(гетерополярную) и ковалентную (гомеополярную).

Ионная связь

Этот вид химической связи обусловлен переносом валентных электроновс одного атома на другой и кулоновским притяжением образовавшихсяионов. Иными словами, ионная связь осуществляется в том случае, ко-гда электроны в молекуле можно разделить на две группы, каждая изкоторых все время находится около одного из ядер. Электроны разде-

32.1. Молекулы

191

ляются так, что около одного из ядер образуется избыток электронов, аоколо другого --- их недостаток, т.е. молекулу можно представить какобразование, состоящее из отрицательного и положительного ионов, при-тягивающихся друг к другу (например, молекула NaCl состоит из ионовNa+ и Cl-

Для описания ионных молекул еще до создания квантовой механики суспехом применялись полуэмпирические способы расчета энергии связи,основанные на классической электростатике. Пусть, например, мы имеемдело с молекулами типа КСl, NaCl и т.п. Обозначим через Um ионизаци-онный потенциал щелочного металла, а через Uh --- сродство галогена кэлектрону. В начальном состоянии имеем два нейтральных атома К и Сl,разнесенные на бесконечно большое расстояние. Попытаемся мысленнопостроить из них молекулу. Затрачивая энергию Um, мы отрываем элек-трон от металла и переносим его на галоген. При присоединении элек-трона к последнему выделится энергия Uh, так что энерговыделение наэтом этапе составляет Uh ---Um. Далее сближаем образованные нами ионыдо равновесного расстояния R0(размер молекулы). При этом выделитсядополнительная энергия кулоновского взаимодействия Ес. Полная вы-делившаяся энергия и есть энергия связи Есв получившейся молекулы:именно ее надо затратить, чтобы разорвать молекулу на составные ча-сти:

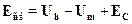
Учитывая, что кулоновская энергия 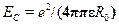,находим отсюда

выражение для равновесного расстояния:

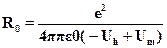
Применим полученную формулу для оценки размера молекулы КС1.Берем экспериментальные данные: Uт = 4.3 эВ, Uh = 3.8 эВ, Есв =4.8 эВ, так что кулоновская энергия Ес = 4.8 --- 3.8 + 4.3 = 5.3 эВ =5.3 х 1.6 10-19 = 8.5 10-19 Дж. Отсюда легко находим размер молекулы:

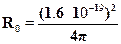
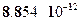
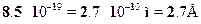
Получившаяся величина примерно в пять раз превышает радиус Бора идает вполне приемлемую оценку размера молекулы.

Глава 32. Физическая природа химической связи

Оценим также размер молекулы другого соединения --- НС1, для ко-торого Uт = 13.6 эВ и Есв = 2.7 эВ. Чтобы не повторять аналогичныхвыкладок, используем уже полученный результат. Имеем в этом случае:Ес = 2.7 --- 3.8 +13.6 = 12.5 эВ, что в 12.5/5.3 ? 2.36 больше кулоновскойэнергии для молекулы КСl. Соответственно, размер молекулы будет втакое же число раз меньшим: R0?2.7 Е /2.36 = 1.1 Е (эксперимент дает

значение R0= 1,3 Е).

Ковалентная связь

Второй вид связи наблюдается в молекулах, где электроны, осуществля-ющие связь, значительную часть времени проводят в пространстве междуатомами и в какой-то мере являются ``общими'' для обоих ядер. Гомео-полярная (ковалентная) связь характерна для большинства молекул сдвумя одинаковыми атомами (H2, N2, О2 и т.п.). Гомеополярная связь неподдается классическому описанию, а требует квантового рассмотрения.

Рассмотрим простейшую гомеополярную молекулу --- молекулу водо-рода. Впервые это было сделано в 1927 г. Гайтлером и Лондоном. Мыограничимся принципиальным анализом, опуская проведение расчетов,т.к. нашей задачей является уяснение физической природы ковалентной(гомеополярной) связи. Схема взаимодействий в такой молекуле, состоя-щей из двух протонов (ядер атома водорода) А и В и двух электронов 1и 2, показана на рис. 32.1.

32.1. Молекулы

193

Рис. 32.1: Схема взаимодействий в молекуле водорода.

Уравнение Шредингера для системы имеет вид:

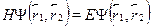
где через 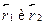обозначены координаты первого и второго электронов,а H --- гамильтониан системы:

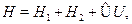
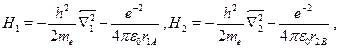
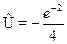
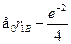
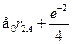
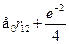
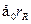
Гамильтониан H1 содержит оператор кинетической энергии электрона1 и потенциальную энергию того же электрона в кулоновском поле ядраА. Аналогичную структуру имеет гамильтониан Я2. Оператор H описы-вает четыре взаимодействия: электрона 1 с ядром В, электрона 2 с ядромА, электронов между собой и ядер --- также между собой. Ядра имеютмассу, примерно в 2000 раз превышающую массу электрона, поэтомуони движутся гораздо медленнее электронов, и в первом приближенииих можно считать неподвижными (такое приближение называется адиа-батическим). Поэтому волновая функция рассматривается какфункция координат только электронов, а расстояние R между ядрами,важное в проблеме ковалентной связи, входит в волновую функцию Фкак параметр. Получающиеся из уравнения Шредингера собственныезначения энергии будут тогда зависеть от расстояния R, т.е. Е=Е(R),причем в случаях параллельной и антипараллельной ориентации спиновэлектронов характер этой зависимости оказывается различным.

Полная волновая функция зависит не только от пространственных ко-ординат электронов, но и от их спинов. Вследствие принципа Паули

Глава 32. Физическая природа химической связи

(согласно которому данный набор квантовых чисел может иметь лишьодна частица), такая полная волновая функция должна быть антисим-метричной относительно перестановки электронов. Поскольку спиновоесостояние не зависит от орбитального, пространственные и спиновые пе-ременные разделяются, и полную волновую функцию электронов в моле-куле водорода можно представить в виде произведения координатной испиновой функций:

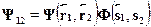
Из принципа Паули следует, что:

• если спиновая волновая функция симметрична, тогда пространствен-ная функция антисимметрична;

• если спиновая волновая функция антисимметрична, тогда простран-ственная функция должна быть симметричной.

Симметричная спиновая волновая функция соответствует параллель-ному расположению векторов спинов электронов, т.е. суммарному спинуэлектронов S = 1. Такое состояние называется триплетным по числу(2S + 1) = 3 возможных проекций суммарного спина. Во втором жеслучае антисимметричная спиновая функция связана с противоположноориентированными спинами, дающими в сумме 5 = 0, и следовательно,возможно только одно значение проекции полного спина, и состояние на-зывается синг летным.

Взаимодействие между нейтральными атомами, когда расстояние меж-ду ядрами R много больше характерных размеров электронных оболочек(т.е. радиуса Бора аB = 4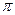

0)2h2) ? ---13.6 эВ. При уменьшении R до нуляэта энергия будет бесконечно возрастать из-за кулоновского отталкива-ния ядер.

Результаты расчетов можно описать следующим образом. Если спиныэлектронов параллельны, то при сближении атомов водорода энергия си-стемы монотонно увеличивается, никакого связанного состояния не воз-никает (кривая Е_ на рис. 32.2). В этом случае предоставленные самимсебе два атома вновь разойдутся, стремясь к состоянию с наименьшейвозможной энергией. Условие существования связанного состояния ---наличие минимума энергии системы при некотором значении Rо --- вы-полняется только при синглетном состоянии электронов, когда их спиныантипараллельны (кривая Е+ на рис. 32.2).

32.1. Молекулы

195

Рис. 32.2: Зависимость энергии Е молекулы водорода от расстояния R между ато-мами. На больших расстояниях имеем два нейтральных атома водорода с общей энергией 2Е0= 2 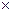( --- 13.6 эВ) = ---27.2 эВ.Кривая Е_ соответствует триплетномусостоянию электронов и проходит выше асимптотического значения2Е0---связан-ного состояния молекулы в этом случаем не существует. Кривая Е+ соответствуетсинглетному состоянию электронов, она имеет минимум при R= Rо (конечный раз-мер молекулы), расстояние которого от асимптотического значения и есть энергиясвязи Есв молекулы водорода.

Понять такое поведение энергии можно на качественном уровне, еслирассмотреть два водородных атома, находящихся на большом расстоя-нии 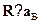друг от друга. Тогда членом взаимодействия Ы в гамиль-

тониане можно пренебречь, и мы имеем два независимых атома,описываемых суммой гамильтонианов H1иH2. Решения соответствую-щего каждому из них уравнения Шредингера мы уже знаем. Введем обо-значения для получающихся волновых функций: Фа(а) и Фвег)- Тогдарешение для суммы гамильтонианов H1 + H2 будет представляться в видепроизведения волновых функций , а энергия --- в виде суммыэнергий, т.е. будет равна 2Е0 - Физический смысл произведения волновыхфункций очевиден: электрон 1 находится в поле ядра А, а электрон 2 --- вполе ядра В. Но электроны неразличимы, и эта физическая ситуация ни-чем не отличается от случая, когда электрон 2 находится в поле ядра А,а электрон 1 --- в поле ядра В. Этому соответствует иное произведениеволновых функций: 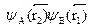, которое тоже является решением урав-нения Шредингера с той же энергией 2Е0 . Согласно принципу суперпо-зиции, решением с этой же энергией будет и любая линейная комбинацияуказанных произведений. Поскольку принцип Паули требует, чтобы пол-

Глава 32. Физическая природа химической связи

ная волновая функция была либо симметрична, либо антисимметричнапо пространственным координатам электрона, она должна иметь вид:

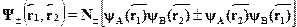
где АД --- вычисляемые нормировочные коэффициенты, обеспечивающиеравенство единице полной вероятности: 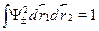. Подставляясюда выражения и учитывая, что и 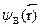уже нормированына единицу, получаем:

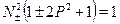
откуда

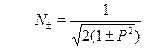
Величина Р, называемая интегралом перекрытия, равна

P=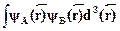

Она характеризует степень перекрытия волновых функци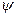й A и 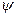B, т.е.степень независимости пространственного распределения электронов другот друга, и играет важную роль в теоретических расчетах свойств мо-лекул.

Если учесть теперь член взаимодействия Ы, то в зависимости от сим-метрии волновой функции Ф 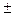получатся поправки к энергии разных зна-ков. В случае антисимметричного состояния 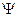_ (полный спин электро-нов S = 1) поправка получается положительной (отталкивание атомов),и связанного состояния не возникает. В случае же симметричного со-стояния 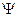+ (полный спин электронов S = 0) поправка для больших Rотрицательна (притяжение атомов), что приводит к образованию моле-кулы водорода.

Осмыслить такое поведение поправки к энергии помогает график вол-новой функции. Ось z направим по линии, соединяющей ядра атомов во-дорода, а начало отсчета выберем в средней точке между ядрами, так чтокоординаты ядра А равны 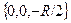, а ядра В 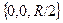. Для про-стоты мы рассмотрим волновые функции на этой оси, причем для случаясимметричного расположения электронов относительно начала отсчет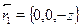а: ., . Тогда

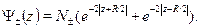
(32.11)

32.1. Молекулы

197

-5-4-3-2-1012345

Рис. 32.3: Волновые функции электронов в молекуле водорода на оси, соединяющейядра атомов для синглетногоФ+и триплетногоФ _состояний.

График этих функций представлен на рис. 32.3.

Мы видим, что в обоих случаях существует наибольшая вероятностьнайти электроны вблизи ядер --- волновые функции имеют экстремумыв точках z = 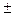R. Однако, при сближении атомов в пространстве междуядрами происходит перераспределение плотности электронов, поведениекоторой различается в зависимости от типа симметрии пространствен-ной части волновой функци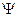и --- + или 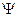_. В состоянии 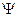+ электронычасть времени проводят в области между протонами (волновая функ-ция в этой области заметно отлична от нуля). В центре между ато-мами получается электронное облачко, притягивающее к себе протоны--- возникает стягивающее действие и образуется молекула. В состоянииже 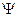_ плотность электронов между протонами уменьшается (волноваяфункция проходит через нуль), отталкивание протонов не экранируется,что и приводит к увеличению энергии системы в этом состоянии (см.рис. 32.2). Положение минимума, таким образом, определяется из реше-ния уравнения Шредингера с учетом потенциальной энергии электриче-ского взаимодействия электронов и протонов в молекуле.

Численные результаты R0 = 0,87 Е, Есв = 3.1 эВ для кривой Е+,полученные в таком подходе, следует сравнить с экспериментальными данными: R0 = 0,74 Е, Есв = 4.5 эВ. Разница в энергии связи составляет31%, в размере молекулы --- 17 %.