Боровская модель атома водорода.

Чтобы получить согласие с результатами наблюдений, Бор предположил, что электрон в атоме водорода движется только по тем круговым орбитам, для которых его момент импульса

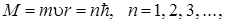(3.12.8)

где n — квантовые числа, т – масса электрона, 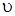- его скорость, r - радиус орбиты. (Рассуждения, которые привели Бора к этому предположению мы опустим.)

С помощью этого правила квантования можно найти радиусы круговых стационарных орбит водорода и водородоподобных систем: ионов атомов с одним оставшимся электроном (Н, Не⁺, Li ^{+ +}, …) и соответствующие им энергии. Пусть заряд ядра водородоподобной системы равен e. Масса ядра значительно больше массы электрона, поэтому ядро при движении электрона можно считать неподвижным. Следуя Бору, будем предполагать, что электрон движется вокруг ядра по окружности радиуса r.

Согласно 2-му закону Ньютона

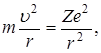(3.12.9)

Решая совместно (3.12.8) и (3.12.9), можно найти радиусы электронных орбит и их скорости на этих орбитах:

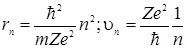. (3.12.10)

Таким образом, радиус первой (ближайшей к ядру) орбиты электрона в атоме водорода (его обозначают обычно 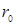и называют первым Боровским радиусом)

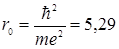нм (3.12.11)

Внутренняя энергия атома складывается из кинетической энергии электрона (ядро полагают неподвижным) и потенциальной энергии взаимодействия электрона с ядром. С учетом (3.12.10) получим:

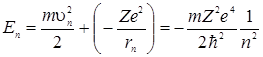. (3.12.12)

При переходе атома водорода (Z =1) из состояния 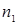в состояние 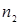излучается фотон

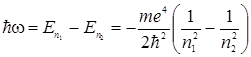. (3.12.13)

Тогда частота испущенного света равна

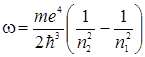, (3.12.14)

Что соответствует обобщенной формуле Бальмера, если постоянная Ридберга определяется 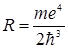. (3.12.15)

Расчет по этой формуле хорошо согласуется с экспериментально определенным значением.

Схема энергетических уровней (разрешенных значений энергии) атома водорода приведена на рис.3.12.4. Там же показаны возможные переходы, сопровождающиеся излучением фотонов определенной частоты.

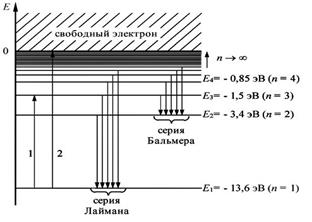
Рис.3.12.4.

Лекция 3.13.