Уравнение Шрёдингера. Квантование энергии и момента импульса. Атом водорода.

Волновая функция. Уравнение Шрёдингера.

В развитие идеи де-Бройля о волновых свойствах вещества Э.Шрёдингер получил в 1926г. свое знаменитое уравнение. Он сопоставил движению микрочастицы комплексную функцию координат и времени, которую назвал волновой функцией и обозначил греческой буквой 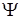. Поэтому ее называют также пси-функцией. Она характеризует состояние микрочастицы. Физический смысл водновой функции состоит в следующем: квадрат ее модуля определяет вероятность нахождения частицы в промежутке между точками х и х+dх в момент времени t. Точнее величина 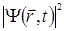является плотностью вероятности или плотностью распределения координат частицы.

Из такого определения следуют свойства волновой функции. Она должна быть однозначной, непрерывной, гладкой (производная не терпит разрыва), конечной. Кроме того, она должна подчиняться условию нормировки .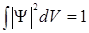

Основная задача физики микрочастиц (волновой или квантовой механики) как раз и состоит в нахождении волновых функций и связанных с ними физических следствий в самых разнообразных условиях. Для ее решения служит волновое уравнение Шрёдингера – основное уравнение нерелятивистской квантовой механики. (Заметим, что одним из решений этого уравнения в свободном пространстве должна быть плоская волна де-Бройля (3.13.9).)

Особое значение в квантовой механике имеют стационарные состояния. Это такие состояния, в которых все наблюдаемые физические параметры не меняются с течением времени. Оказывается, что в стационарных состояниях

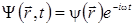, (3.14.1)

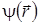где частота постоянна, а функция не зависит от времени. Эта независящая от времени часть волновой функции может быть найдена из уравнения Шрёдингера для стационарных состояний

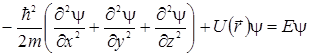, (3.14.2)

где т - масса частицы, Е – ее энергия, 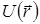- функция, которая в случае стационарных состояний имеет смысл потенциальной энергии частицы.

Энергия частицы Е входит в уравнение в качестве параметра. В теории дифференциальных уравнений доказывается, что уравнения вида (3.14.2) имеют решения, удовлетворяющие стандартным условиям, не при любых значениях параметра Е, а лишь при некоторых избранных значениях. Эти избранные значения называются собственными значениями энергии. Решения (значения волновой функции), соответствующие собственным значениям Е, называются собственными функциями. Совокупность собственных значений называется спектром величины (энергии). Если эта совокупность образует дискретную последовательность, спектр называется дискретным, если же – непрерывную последовательность, спектр непрерывный или сплошной.

Таким образом, из основных положений квантовой механики без каких-либо дополнительных предположений следует квантование (дискретность) энергии.

Частица в бесконечно глубокой потенциальной яме.

Рассмотрим квантование энергии на простейшем примере движения частицы, находящейся в бесконечно глубокой одномерной потенциальной яме. Пусть частица может двигаться только вдоль оси х, где движение ограничено непроницаемыми для частицы стенками: х = 0 и х = l. Потенциальная энергия рана нулю при 0≤ х ≤ l и обращается в бесконечность при х < 0 и x > l .

Поскольку волновая функция в этом случае будет зависеть только от х, уравнение Шрёдингера будет иметь вид

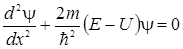. (3.14.3)

За пределы потенциальной ямы частица попасть не может. Поэтому вероятность обнаружить там частицу, а, следовательно, и волновая функция в этих областях равна нулю. Из условия непрерывности следует, что и на границах ямы она равна нулю

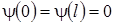. (3.14.4)

В области, где 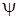не равна тождественно нулю, уравнение (3.14.3) примет вид 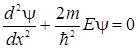. (3.14.5)

Введя обозначение 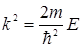, (3.14.6)

получим уравнение 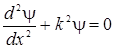, (3.14.7)

решение которого будет иметь вид

. (3.14.8)

Из первой части условия (3.14.4) следует 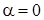. Вторая часть этого условия

Будет выполнена лишь в случае, если

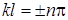(n=1,2,3,…), (3.14.9)

откуда, приняв во внимание (3.14.6), найдем собственные значения энергии частицы 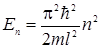(п=1,2,3,…). (3.14.10)

Спектр энергии оказался дискретным.

Оценим «расстояния» между соседними уровнями. Разность энергий между двумя соседними уровнями равна

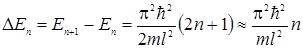. (3.14.11)

Если оценить эту величину для молекулы газа в сосуде (т ~ 10 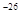кг, l ~ 10cм), получим 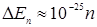Дж 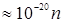эВ. Столь густо расположенные энергетические уровни будут практически восприниматься как сплошной спектр энергии, так что, хотя квантование энергии в принципе будет иметь место, на характере движения молекул это сказываться не будет. 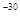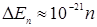Аналогичный результат получим, если рассмотреть поведение свободных электронов в металле (те же размеры ямы, т ~ 10 кг, Дж 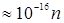эВ). Однако, совсем другой результат получится для электрона, если область, в пределах которой он может двигаться, будет порядка атомных размеров (~ 10 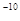м). В этом случае

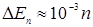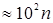Дж эВ,

так что дискретность энергетических уровней будет весьма заметна.

Атом водорода.

Рассмотрим систему, называемую водородоподобным атомом, состоящую из неподвижного ядра с зарядом Ze и движущегося вокруг него электрона (при Z=1 – это атом водорода). Потенциальная энергия электрона представляет собой в этом случае сферически симметричную функцию

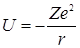. (3.14.12)

Такой случай не предусматривался теорией Бора. В ней движение электрона вокруг ядра происходило по плоским орбитам. Но в квантовой механике, в которой нет представления о движении электронов по орбитам, нет препятствий для реализации сферически симметричных состояний атома. Поэтому уравнение Шрёдингера целесообразно записать в сферической системе координат: r, 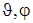. Решая это уравнение, получим, что собственные значения энергии могут принимать 1)любые положительные значения 2) дискретные отрицательные значения, равные 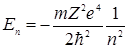(п=1,2,3,…). (3.14.13)

Случай Е > 0 соответствует электрону, пролетающему вблизи ядра и удаляющемуся на бесконечность. Случай Е < 0 - электрону, связанному с ядром. Заметим, что полученное выражение (3.14.13) совпадает с соответствующей формулой теории Бора (3.12.12). Однако в квантовой механике эти значения получаются из решения основного уравнения без введения каких-либо дополнительных предположений.

Собственные функции уравнения Шрёдингера оказываются от трех целочисленных параметров, которые принято обозначать п, l, т, и распадаются на два множителя, один из которых зависит только от r, другой – от углов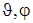

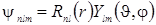. (3.14.14)

Параметры п, , т называются квантовыми числами. Параметр п называется главным квантовым числом и совпадает с номером уровня энергии в (3.14.13). Параметр l называется азимутальным (или орбитальным) квантовым числом и может при заданном п принимать значения

l = 0,1,2,…(n-1). (3.14.15)

Параметр т - магнитное квантовое число может иметь значения

т = -l, -l+1,…,-1, 0, +1,…,l – 1, l. (3.14.16)

Используя условие нормировки и вид 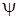- функции (3.14.14) и проинтегрировав ее по всем возможным углам 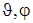, можно найти вероятность обнаружить электрон на расстоянии от ядра. На рис. 3.14.1 приведены графики плотности вероятности для атома водорода для состояний 1s (п =1, l = 0) и 2s (п = 2, l = 0), 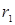- первый боровский радиус. Пунктирами отмечены радиусы соответствующих боровских орбит. Из рисунка видно, что эти радиусы совпадают с наиболее вероятными расстояниями электрона от ядра. Следовательно, в квантовой механике радиус первой боровской орбиты надо истолковать.как такое расстояние от ядра, на котором вероятность обнаружения электрона максимальна. Таким образом, атом водорода можно представить в виде сферически симметричного электронного облака, в центре которого находится ядро.

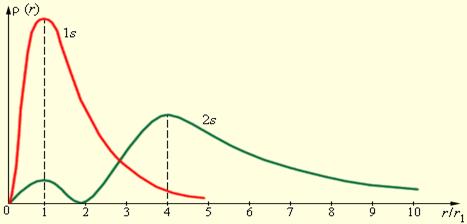
Рис.3.14.1.

Из уравнения Шрёдингера следует также, что квантованным будет и момент импульса электрона. Поскольку, как уже говорилось ранее, все три проекции момента импульса одновременно не могут быть определены, то определяют модуль момента импульса М и его проекцию на одну из осей М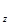

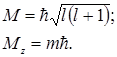(3.14.16)

Из этих формул вытекает, что М 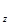< M. Следовательно, направление момента импульса не может совпадать с выделенным в пространстве направлением. Это согласуется с тем обстоятельством, что направление механического момента в пространстве является неопределенным.

При переходе атома из одного состояние в другое изменяется его энергия, что сопровождается излучением или поглощением фотона. Так как фотон имеет не равный нулю момент импульса, то момент импульса атома должен соответственно измениться. Поэтому возможны только такие переходы, при которых азимутальное квантовое число изменяется на единицу

.

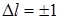Лекция 3.15