Низкий бесконечный барьер
Потенциальная энергия имеет вид:
U(x)= 
Слово "низкий'' означает, что высота барьера U меньше энергии частицыЕ (рис. 30.1). Решим уравнение Шредингера отдельно для каждой изобластей. В области 1 потенциал равен нулю и мы имеем то же общеерешение для свободной частицы:
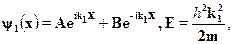
Глава 30. Уравнение Шредингера
Рис. 30.1: Низкий потенциальный барьер, пунктиром показана энергия налетающейслева частицы, цифрами---номера областей с различной потенциальной энергией
где А и В --- амплитуды падающей и отраженной волны, соответственно.В области 2 уравнение Шредингера имеет вид:
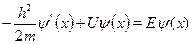
В этой области меняется кинетическая энергия (и импульс) частицы, имы должны ввести другой волновой вектор (обозначим его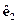 
в отличиеот прежнего 
):
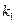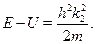
Тогда очевидно, что решение уравнения Шредингера в области 2 будетиметь тот же вид, что и для области 1 с заменой 
на 
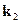. Однако изфизических соображений ясно, что в области 2 не может быть волны,распространяющейся справа налево (в бесконечно удаленной точке ей неот чего отражаться). Поэтому волновая функция в этой области соот-ветствует прямой волне:
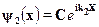
По сути дела, здесь мы снова использовали некое граничное условие,хотя и иное, нежели для задачи о связанном состоянии. Нам осталосьопределить только амплитуды А,В,С.
Для этого мы должны вспомнить, что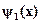 
и 
--- значения однойволновой функции в разных пространственных областях. Эта волноваяфункция должна быть непрерывна вместе со своей первой производнойпо переменной х. Непрерывность функции в точке х = 0 означает, чтодолжно выполняться условие
? 
?
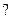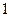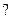
2, откуда А + В = С.
Непрерывность первой производной волновой функции означает выпол-нение равенства
= 
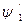(0) , откуда k1(А --- В)= k2С .
30.7. Отражение и туннелирование частиц
145
Решение двух полученных уравнений дает
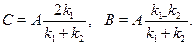
Амплитуда падающей волны остается не определенной: ясно, что оназависит от интенсивности потока частиц. Важны не сами амплитуды, аотношение R квадратов их модулей, т.е. интенсивностей отраженной ипадающей волн:
Величина R называется коэффициентом отражения частицы от низкогобарьера. По физическому смыслу это --- вероятность отражения частицы
называемая коэффициентом прохождения, определяет вероятность про-никновения частицы в правую область. Удивительно, что частица имеетшанс отразиться от низкого барьера и повернуть назад. В классическойфизике частица всегда (R = 0) проникает за барьер, если ей хватает наэто энергии. Например, с точки зрения классической физики электрон сэнергией 10 эВ, влетевший в конденсатор с тормозящим полем 5 В без-условно преодолеет торможение и продолжит свой путь с уменьшеннойэнергией 5 эВ. В квантовой же теории не равна нулю вероятность того,что электрон отразится от поля конденсатора и повернет назад. Коэф-фициент отражения можно измерить, направляя поток частиц на барьери измеряя долю отраженных от него частиц.
Дата добавления: 2016-01-26; просмотров: 1008;