Свободная частица, движущаяся вдоль оси х
Потенциальная энергия равна нулю (U(х) = 0), и производные по у и zв операторе Лапласа исчезают. Уравнение принимает вид:
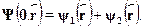
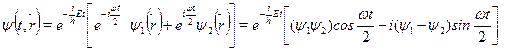
Введем волновой вектор k: Е=h2k2/2m, и перепишем уравнение в виде
Глава 30. Уравнение Шредингера
Существует, как известно, два линейно независимых решения ,так что общее решение есть суперпозиция волн: стоячих
(первый член --- волна направо, второй --- налево; постоянные АиВпроизвольны). Аналогия: такие же решения описывают колебания сво-бодной струны. Поскольку возможны волны с произвольной частотой,то струна не звучит (т.е. энергия частицы не квантуется). Для ча-стицы, движущейся в произвольном направлении вдоль волнового век-тора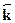 
, справедливы те же решения при замене kx> 
.
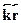При решении большинства задач квантовой механики следует обра-тить внимание, что волновая функция должна быть непрерывной --- ве-роятность пребывания частицы не может меняться скачком от точки кточке. Если потенциал конечен, то из уравнения Шредингера следует,что первая производная также непрерывна.
Дата добавления: 2016-01-26; просмотров: 711;