Определение момента инерции маховика для V-образного ДВС
Кинематическая схема механизма двигателя и расчетная нагрузочная диаграмма приведены на рис. 10 и 12. В качестве других исходных данных приняты: коэффициент неравномерности движения d = 0,2; размеры звеньев: r = lОА = 0,13м; lАВ = lАС = 0,43м; положения центров масс звеньев 2 и 4: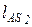 
= 
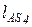= lAB/3; массовые характеристики: m2 = m4 = 3,2 кг; m3 = m5 = 3,6 кг; JS1 = 0,16 кгм2; JS2 = JS4 = 0,08 кгм2; частота вращения кривошипного вала n = 2400 об/мин. Угловая скорость звена приведения кривошипа ОА: 
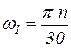= 251,3 c-1.
Для каждого положения механизма определяем приведенный момент инерции звеньев механизма по формуле (16), которая в рассматриваемом случае принимает вид
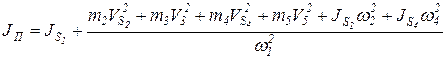. (64)
Линейные и угловые скорости звеньев механизма определяются из планов скоростей. Для определения скоростей звеньев механизма можно воспользоваться повернутыми планами скоростей, показанными, в частности, для 4, 8 и 11 положений механизма на рис. 13. Угловые скорости w2 и w4 звеньев 2 и 4 определяются по соотношениям
; 
,
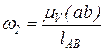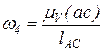где (ab), (ac) – длины в мм отрезков ab и ac на планах скоростей, отражающие скорости точек B и C механизма относительно точки А.
В некоторых положениях механизма, в частности в положении 4 (рис. 10), скорости точек А4, В4 (см. план скоростей на рис. 13, в) одинаковы, скорость точки В4 относительно А4 равна нулю и соответственно угловая скорость w 2 = 0. Аналогичные положения существуют и для скорости w3, в которых она также равна нулю.
По полученным значениям JП строится график приведенного момента инерции механизма JП(j) в зависимости от угла поворота кривошипа с направлением оси абсцисс φ – по вертикали от начала координат вниз (на рис. 37, а – от начала О2п), а оси ординат по горизонтали вправо.
После построения JП(j) определяются значения и строятся графики приведенных моментов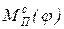 
, 
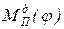и работ 
, 
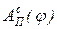сил движущих и сил сопротивления (рис. 37, б, в). Эти графики в рассматриваемом примере были получены при обработке индикаторной диаграммы двигателя в разделе 4.2.2 (рис. 14).
Как было отмечено в этом разделе, силами веса звеньев при обработке индикаторной диаграммы двигателя можно было пренебречь ввиду их малости по сравнению с заданными силами РI и РII. Действительно, в данном примере максимальный вес звеньев механизма – вес поршней при массе 3,6 кг составляет G3 = G5 = 3,6×9,81 = 35,32 Н; максимальные усилия РI = РII = 79200 Н, то есть максимальный вес звеньев не превышает 0,05%.
На практике, в том числе и при выполнении курсового проекта, если силы веса звеньев составляют не более 1% от заданных сил, их при определении приведенных моментов и работ сил движущих и сил сопротивления можно не учитывать.
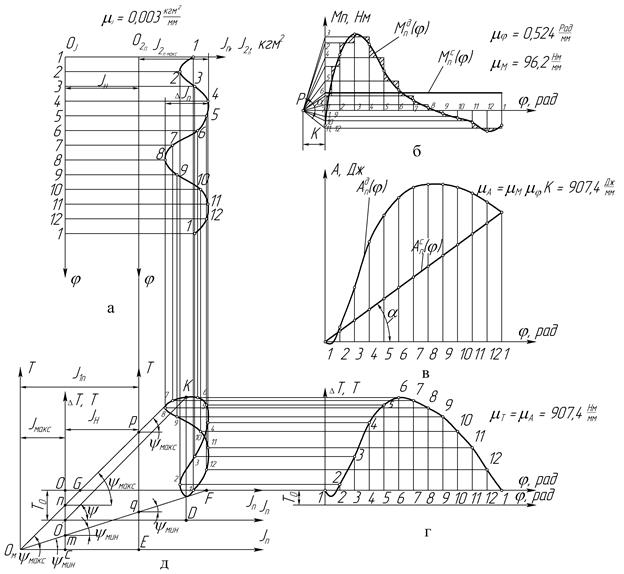
Рисунок 37 – Последовательность «а», «б»… «д» построения графиков
при определении момента инерции маховика
По разнице работ , 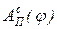приведенных моментов сил движущих и сил сопротивления определяются приращения DТ = - 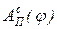и строится график изменения кинетической энергии механизма DТ(j) за цикл установившегося движения (рис.37, г).
Значения DТ соответствуют значениям интеграла в подкоренном выражении правой части уравнения (27), из решения которого определяется изменение угловой скорости кривошипа w1 за цикл установившегося движения.
Как следует из уравнения (37), для определения момента инерции маховика необходимо определить значения максимальной w1макс и минимальной w1мин угловых скоростей кривошипа за цикл установившегося движения. Эти значения определяются в системе координат DТОJП из диаграммы «энергия-масса» DТ(JП) (диаграммы Виттенбауэра) (рис.37, д), которая строится на основании графиков JП(j) (рис.37, а) и DТ(j) (рис.37, г). Построение выполняется путем графического исключения параметра j (угла поворота кривошипа) из графиков JП(j) и DТ(j). Точки диаграммы DТ(JП) получаются на пересечении прямых параллельных горизонтальной оси абсцисс графика DТ(j) и вертикальной оси абсцисс графика JП(j), проведенных через одноименные точки этих графиков, соответствующие положениям механизма. Полученные точки соединяют плавной кривой и получают диаграмму «энергия-масса».
Покажем, что на основании диаграммы «энергия-масса» можно определить максимальную wмакс и минимальную wмин угловые скорости кривошипа.
Если отложить значение кинетической энергии механизма Т0 в начале цикла установившегося движения при j = 0 от начала координат (точка 0) графика DТ(JП) вниз, то получим точку 0' – начало координат графика изменения полной кинетической энергии Т(JП) (рис.37, д). Для любой точки К этого графика, соединив ее прямой линией с началом координат 0¢ и проектируя точку К в точку D на ось абсцисс, из треугольника 0'КD получим
,
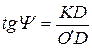но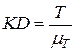 
, 
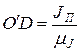
и с учетом этих выражений получаем
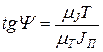, (65)
где Y – угол между отрезком 0'К и осью абсцисс графика Т(JП).
Подставляя в это выражение значение кинетической энергии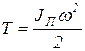 
, после преобразований получим формулу для определения угловой скорости звена приведения
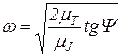. (66)
По этой формуле можно определить угловую скорость звена приведения в любом положении механизма за цикл установившегося движения, в том числе wмакс и wмин, то есть найти закон движения звена приведения w = w(j).
Из формулы (66) следует, что wмакс и wмин соответствуют максимальному и минимальному углам Yмакс и Yмин, которые, в свою очередь, соответствуют углам наклона к оси абсцисс касательных, проведенных из начала координат 0' к графику Т(JП).
Уравнениями (31), приведенными в разделе 1, установлены зависимости wмакс и wмин от заданных значений d и wср. Подставляя значения wмакс и wмин из (31) в формулу (66), получим
; 
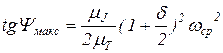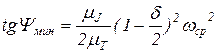. (67)
Ввиду малости значения d в сравнении с единицей, пренебрегая величиной второго порядка малости 
, эти выражения приобретают вид
; 
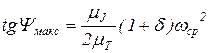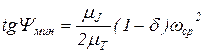. (68)
По этим формулам вычисляют значения Yмакс и Yмин и проводят касательные к диаграмме Виттенбауэра Т(JП) под углами Yмин с нижней стороны диаграммы и Yмакс с верхней. Пересечение касательных определяет положение начала Ом новой системы координат ТОмJП (см. также рис. 3), которая соответствует условию работы механизма с заданным коэффициентом неравномерности движения d при установке на кривошипном валу механизма маховика. Величина момента инерции маховика Jмах определяется длиной отрезка ОмС (рис.37, д) в миллиметрах и вычисляется по выражению
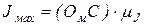. (69)
При выполнении курсового проекта может оказаться, что начало новой системы координат Ом из-за небольшой разницы углов Yмин и Yмакс может выходить за пределы формата листа графической части проекта. В частности, в рассматриваемом примере значения этих углов составляют Yмин = 5,8° и Yмакс = 7,1° и точка Ом может располагаться за пределами чертежа. На рис. 37, д точка Ом условно показана в пределах чертежа для понимания сути рассматриваемого вопроса. В случаях выхода начала координат Ом за пределы чертежа момент инерции маховика определяется по длине отрезков на координатных осях, образуемых между точками их пересечения касательными, проведенными к диаграмме Виттенбауэра под углами Yмин и Yмакс. В рассматриваемом примере искомый отрезок (OмС) определится в зависимости от длины отрезка (mn) между точками m и n пересечения касательных с осью ординат из следующих соотношений:
; 
; 
;
; 
.
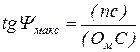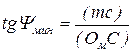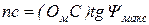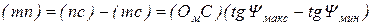Отрезки в скобках измеряются в миллиметрах на чертеже.
В результате получаем
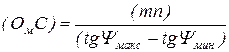. (70)
Подставляя в (70) выражения для tg(Yмакс) и tg(Yмин) из (68), после преобразований и последующей подстановки в (69) получаем формулу для определения момента инерции маховика
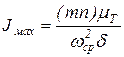. (71)
Для рассматриваемого примера: (mn) = 62 мм;
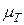= 907,4 Нм/мм; 
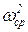= 63152 с-2; d = 0,2 и момент инерции маховика
= 
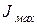кгм2.
У некоторых машин постоянная часть приведенного момента инерции механизма JН (см. формулу (34)) значительно превышает изменение DJП (см. рис. 37, а) переменного приведенного момента инерции звеньев второй группы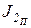 
(j) (см. формулу 32)). В этом случае изменение DJП в принятом масштабе может оказаться весьма малым и, как уже отмечено выше, диаграмма Виттенбауэра DТ(JП) (рис. 37, д) может быть настолько сужена, что точно провести касательные для определения углов Yмин и Yмакс и определить момент инерции маховика окажется невозможным. В этом случае момент инерции маховика Jмах можно определить из графика изменения приведенного момента 
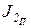(j) механизма, построив его в системе координат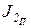 
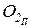j (см. рис. 37, а) без учета постоянной части JН, которая вычисляется предварительно. Длина отрезка (OмС) = (OмЕ) – (СЕ) определяет величину момента инерции маховика
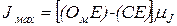, (72)
и аналогично определению через отрезок (mn), момент инерции маховика может быть определен через отрезок (pq) из выражения
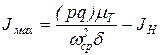. (73)
Эта формула эквивалентна выражению (37) для определения момента инерции маховика аналитическим методом.
Для определения Jмах по формуле (73) без учета постоянной части JН определяют значения переменной части приведенного момента инерции 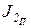и строят диаграмму «энергия-масса» в системе координат TEJП (см. рис.37, д), направляя ось ординат ЕТ навстречу оси абсцисс j графика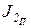 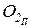j (рис. 37, а). Под углами Yмин и Yмакс к оси JП из начала координат Ом проводят касательные к диаграмме, определяют точки р и q их пересечения с осью ординат ЕТ и по длине отрезка (pq) по формуле (73) находят момент инерции маховика.
При определении момента инерции маховика по формуле (73) за счет подбора соответствующего масштабного коэффициента mJ и уменьшения площади, занимаемой графиком 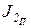(j) в системе координат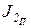 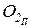j (рис. 37, а), можно увеличить величину изменения DJП приведенного момента инерции механизма на графике без увеличения площади, занимаемой графиком, и построить диаграмму «энергия-масса» в более представительном изображении.
Если в составе механизма имеются вращающиеся звенья, связанные со звеном приведения через промежуточные вращающиеся звенья, то постоянная часть приведенного момента инерции механизма JН определяется как сумма момента инерции этих звеньев с учетом передаточного отношения между ними.
В рассмотренном примере определения момента инерции маховика для V-образного двигателя внутреннего сгорания касательные к диаграмме «энергия-масса» пересекают оси ординат в точках m, n или p, q (рис. 37, д). На практике возможны случаи, когда касательные расположены под углами Yмин и Yмакс к оси абсцисс близкими к 90º и могут не пересекать ось ординат в пределах чертежа. Тогда отрезок (mn) определяется в системе координат DТОJП из треугольников ОmF и ОnG (рис. 37, д) по выражению
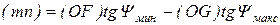, (74)
где (OG) и (OF) – расстояния от начала координат О до точек G и F пересечения касательных с осью абсцисс ОJП, проведенных под углами Yмин и Yмакс к диаграмме «энергия-масса».
Дата добавления: 2016-01-07; просмотров: 1436;