Поскольку в задаче нет характерного линейного размера, скорость найденных волн Рэлея не зависит от длины волны и от частоты, т.е. дисперсии волн нет.

Рассмотрим движение частиц в волнах Рэлея. Для этого необходимо найти действительные перемещения. Поскольку определитель системы (4.8.7) равен нулю, комплексные коэффициенты связаны соотношением 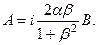Выделяя действительную часть в решениях (4.8.3), получим:

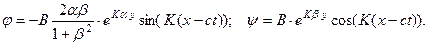
Перемещения будут равны:

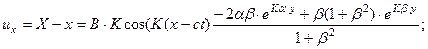
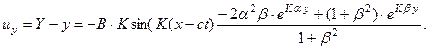
Переменными обозначены текущие координаты частицы, которая в невозмущенном состоянии имела координаты После простых преобразований находим уравнения траекторий частиц. Они представляют эллипсы, полуоси которых меняются с глубиной и при больших значениях глубины стремятся к нулю как экспоненты.

Исследуем характер изменения полуосей от глубины:

,

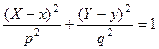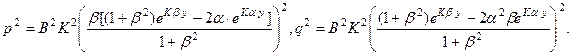
Рассмотрим их изменение при , когда

.

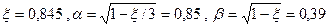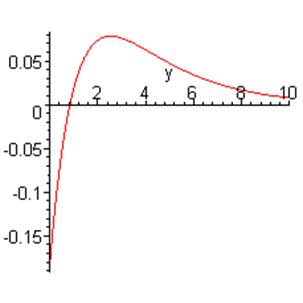
Рис.4.5 Зависимость от глубины .

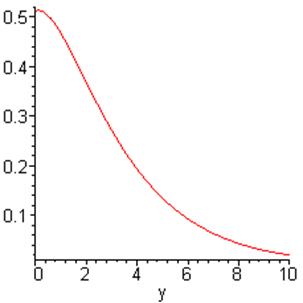
Рис.4.6 Зависимость от глубины .

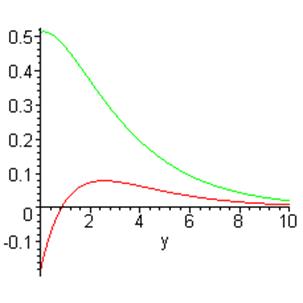
Рис.4.7 Сравнение графиков зависимости безразмерных смещений от глубиныKy.

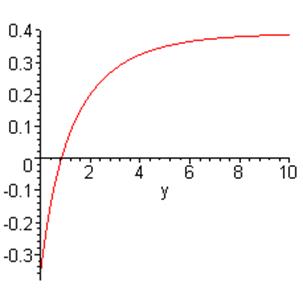
Рис.4.8 Отношение перемещений в зависимости от глубины.

Дальнейшие исследования по этому вопросу принадлежат Бромвичу и Ламбу. Первый из них показал, что результаты, полученные Релеем, не изменяются существенно, если принять во внимание силу тяжести. Второй рассмотрел эффект начального возму­щения, ограниченного некоторой областью на границе или вблизи нее. Он показал, что на некотором расстоянии от источника возмущение начи­нается по истечении промежутка времени, необходимого для распростране­ния продольной волны. Вторая стадия движения начинается по истечении промежутка времени, соответствующего распространению поперечной волны, и, наконец, возмущение с гораздо большей амплитудой начинается по истечении промежутка времени, соот­ветствующего распространению волн типа, исследованного Релеем. Теория поверхностных волн была распространена Ламбом на случай твердого тела, ограниченного двумя параллельными плоскостями.

Волны Лява.

На предыдущем параграфе были рассмотрены волны, бегущие вдоль свободной поверхности однородной упругой среды – волны Рэлея. Оказалось, что их скорость не зависит от длины волны и определяется только физическими характеристиками среды: плотностью, модулем Юнга и коэффициентом Пуассона. Этот результат логичен, поскольку в задаче отсутствовал характерный линейный размер.

Рассмотрим пример задачи, в которой характерный линейный размер входит непосредственно в саму постановку. Будем искать волны поперечной поляризации, бегущие по упругому слою, лежащему на полупространстве, заполненном более жестким упругим материалом (рис.4.9).

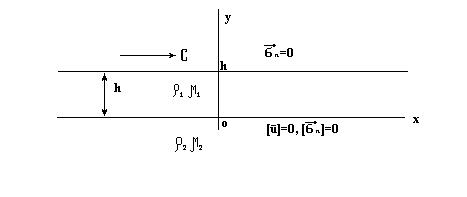
Рис.4.9 Волны Лява в упругом слое 0<y<h , лежащем на упругом основании y<0.

Уравнения движения упругой среды в перемещениях в случае отсутствия массовых сил имеют вид: 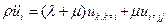. (4.9.1)

Будем искать решение в виде волн поперечной поляризации, несущих возмущение единственной составляющей вектора перемещений 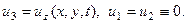При этом сами волны распространяются в плоскости 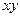и затухают с глубиной, т.е. при 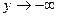. Подстановка единственной отличной от нуля компоненты вектора перемещений приводит к волновому уравнению:

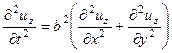, (4.9.2)