Общее решение, которого представляется в виде суммы двух бегущих в противоположном направлении волн

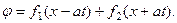
При этом профиль и амплитуда волны не меняется. Если искать ограниченные решения методом Фурье путем разделения переменных 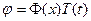, получим 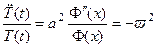, откуда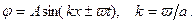

Величина круговая частота колебаний, k- волновое число, длина волны, период колебаний, частота колебаний.

Групповая скорость волн. Пока мы рассматривали лишь монохроматические волны, т. е. синусоидальные колебания, за­данные на бесконечном временном интервале и имеющие по­стоянные амплитуду и частоту. Взятые в таком чистом, идеаль­ном виде, эти волны представляют мало интереса для практики. В самом деле, наблюдатель, который следит за распространени­ем монохроматической волны, получает не больше сведений от этого процесса, чем от наблюдения за стабильным течением од­нородного потока жидкости. Передача информации связана с введением некоторой аномалии, некоторого изменения определен­ных характеристических параметров. Поток жидкости может нести сообщение либо когда по нему, например, плывет щепка, либо если он становится менее или более полноводным. Точно так же для передачи информации с помощью волны необходимо изменять хотя бы один из двух ее параметров: амплитуду или фазу. Такая несущая информацию сложная волна не является уже монохроматической, так как, либо ее амплитуда, либо ча­стота оказываются промодулированными передаваемым сигналом, но ее можно представить в виде суммы бесконечного числа монохроматических волн с различными амплитудами и частотами (группа волн или волновой пакет).

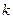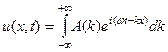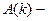Выбирая в качестве переменной волновое числоk,получаем волновой пакет в виде интеграла Фурье по переменной : , где спектральная плотность амплитуды волнового пакета. Если фазовая скорость волн зависит от частоты, то среда, в которой распространяются волны, обладает дисперсией волн. В среде с дисперсией волн пакет волн размывается по мере их распространения. Рассмотрим пакет волн в среде с дисперсией. Обычно частота несущей волны ве­лика по сравнению с частотой модулирующего сигнала, а величина спектральной плотности 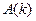имеет существенную величину лишь в окрестности некоторого волнового числа 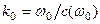, тогда частоту колебаний можно разложить в окрестности 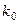, ограничившись первым членом разложения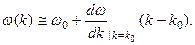

Введем величину 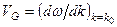, (4.п.2)

имеющую размерность скорости. Тогда спектральное представление пакета волн примет следующий вид:

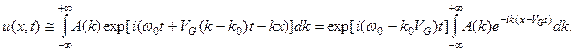
Если ввести обозначения 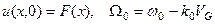, то его можно представить в форме 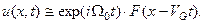(4.п.3)

Выражение (4.п.3) показывает, что за время 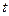группа волн смещается на расстояние 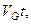таким образом, в среде, обла­дающей дисперсией, волновой пакет с центральным значением волнового числа 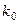распространяется с групповой скоростью 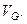В случае, когда среда обладает дисперсией, волновой пакет искажается по мере распространения. Этот результат не следует непосредственно из полученных выше формул, так как при их выводе мы ограничились лишь первым порядком в разложении дисперсионного соотношения. Искажения могут быть связаны, например, с тем, что высокочастотные составляющие, формирую­щие фронт сигнала, будут распространяться медленнее низкоча­стотных составляющих, относящихся к слабо изменяющейся части сигнала (вершине импульса, например). В таком случае вершина импульса как бы перегоняет фронт сигнала. Максимум такой группы волн находится в некоторый момент времениt в точке координатойх, характерной тем, что здесь, интерферируя, складываются волны наибольшей амплитуды. Для такого сложе­ния необходимо, чтобы составляющие с волновыми числами вбли­зи 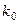оказались в фазе, т. е. при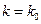

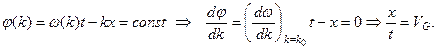
Как видно, и этот метод, называемый методом стационарной фазы, снова показывает, что основная часть волнового пакета перемещается со скоростью, равной 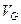, т.е. с определенной нами групповой скоростью. В отсутствие затухания эта скорость представ­ляет собой и скорость переноса энергии волнового пакета.