Приложение к разделу 4.

Общие свойства волн. Любое локальное нарушение равновесия среды создает распространяющееся в ней возмущение, т.е. бегущую волну. Для описания волны используют следующие параметры: скорость, частота и волновой вектор, причем их определения не зависят от природы возмущения. В случае ограниченной среды бегущая волна отражается на границах.

Плоская бегущая волна. Для наблюдения за распростра­нением какого-либо возмущения необходимо в некоторой фикси­рованной точке пространства реги­стрировать изменения во времени соответствующей характерной ве­личины. Для наблюдателя, нахо­дящегося в точке с координатой 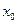, эта величина в момент време­ни 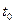принимает значениеи. Допустим, что возмуще­ние не изменяется в процессе распространения, например, не за­тухает, а лишь перемещается с постоянной скоростьюа, тогда величинаиимеет одинаковые зна­чения в точкахх в моменты вре­мениt , удовлетворяющие соотно­шению 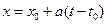. Функцияu(x,t),описывающая данное явление, зависит лишь от величиныt-x/a, так как она принимает одни и те же зна­чения для любыхх иt при постоянной величинеt-x/a, т. е.u(x,t)=F( t-x/a). Эта функцияF( t-x/a) описывает волну, бегущую в положитель­ном направлении осих. Если же распространение происходит в отрицательном направлении, то u(x,t)=F( t+x/a). При одновременном распространении в одной среде волн, бе­гущих в противоположных направлениях, получается результи­рующее возмущение

u(x,t)=F( t-x/a)+ G( t+x/a)

Среди всех возможных видов возмущений особенно большое значение имеют синусоидальные колебания около некоторого среднего положения, поскольку возмущения других видов можно рассматривать как суперпозицию синусоидальных колебаний.

Рассмотрим акустическую волну, излучаемую плоской мемб­раной, совершающей синусоидальные колебания:u=Acos(wt). На расстояниих от начала координат эта волна будет иметь видu=Acos(w(t-x/a)), где величинаи обозначает смещение некоторой плоскости среды, но она может также представлять изменение давления или плот­ности в некотором сечении, параллельном плоскости мембраны. 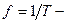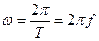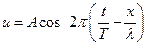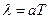Если черезТ обозначить период колебаний, то ча­стота, которая следующим образом связана с круговой частотой: и предыдущее уравнение можно записать в виде где — длина волны, т. е. расстояние, на которое распрост­раняется возмущение за один период. Поскольку через промежу­ток времениТ состояние исследуемой системы повторяется, то в каждый данный момент времени длине волны 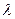соответствует расстояние, разделяющее одинаковые состояния среды, например два последовательных максимума величиныи. Выражение для волны удобно также записывать в виде 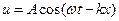, гдеk называется волновым числом. Величинаkx в каждый момент времени характеризует сдвиг фаз в точкех относительно начала координат, в нашем случае это сдвиг фаз между колебаниями в точкех среды и колебаниями мембраны. Введем обобщенную фазу волны 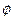: 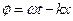, тогда волновое числоkсвязано с изменением фазы 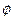в зависимости от расстояниях в данный момент времени как 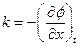, а круговая частота 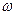выражается через изменение фазы во вре­мени в данной точке в виде .

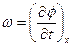Таким образом, существует определенное пространственно-временное соответствие:

Время	Пространство
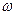
ПериодТ Круговая частота	Длина волны 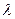Волновое числоk

Скорость распространения возмущения называется фазовой скоростью. Это скорость, с которой должен переме­щаться наблюдатель для того, чтобы в каждый момент времени видеть колебание в одной и той же фазе, т. е. . Волна при этом представляется неподвижной.

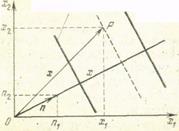
В предыдущем примере частицы, расположенные в плоскости, параллельной плоскости мембраны колеблются в фазе, и движе­ние в каждой точке этой плоскости волнового фронта определено, по­скольку дано расстояниехот нача­ла координат. Для описания коле­бательного состояния в некоторой точкеР, определенной векторомОР, соединяющим начало коор­динат с этой точкой, нужно ввести единичный вектор , перпендикулярный к волновым фронтам. И тогда в случае плоской синусоидальной волны имеем , где введен волновой вектор .