Закон Архимеда и его приложение
Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление, направленное снизу вверх и равное весу жидкости в объеме погруженной части тела.
Pвыт = ρжgVпогр
Для однородного тела плавающего на поверхности справедливо соотношение
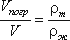
где: V - объем плавающего тела;
ρm - плотность тела.
Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.
Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется устойчивостью. Вес жидкости, взятой в объеме погруженной части судна называют водоизмещением, а точку приложения равнодействующей давления (т.е. центр давления) - центром водоизмещения. При нормальном положении судна центр тяжести С и центр водоизмещения d лежат на одной вертикальной прямой O'-O", представляющей ось симметрии судна и называемой осью плавания (рис.2.5).
Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна KLM вышла из жидкости, а часть K'L'M', наоборот, погрузилось в нее. При этом получили новое положении центра водоизмещения d'. Приложим к точке d' подъемную силу R и линию ее действия продолжим до пересечения с осью симметрии O'-O". Полученная точка m называется метацентром, а отрезок mC = h называется метацентрической высотой. Будем считать h положительным, если точка m лежит выше точки C, и отрицательным - в противном случае.
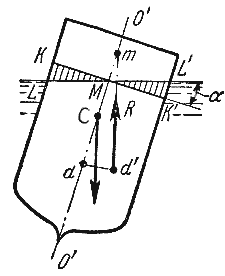
Рис. 2.5. Поперечный профиль судна
Теперь рассмотрим условия равновесия судна:
1) если h > 0, то судно возвращается в первоначальное положение;
2) если h = 0, то это случай безразличного равновесия;
3) если h<0, то это случай неостойчивого равновесия, при котором продолжается дальнейшее опрокидывание судна.
Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше будет остойчивость судна.
Дата добавления: 2015-12-29; просмотров: 791;
