Если рассматривать упругое полупространство со свободной границей, на границе должен быть равен нулю вектор напряжений

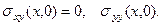(4.8.4)

Учитывая представление Ламе для перемещений, выражения для деформаций и закон Гука, напряжения, входящие в граничные условия можно представить в виде:

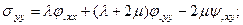
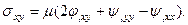
Или с учетом значения скоростей продольных и поперечных волн:

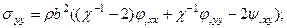
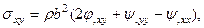(4.8.5)

где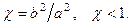

Подстановка решений (4.8.3) в (4.8.5) дает:

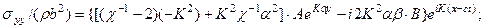
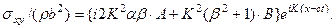
Учитывая (4.8.2), получим

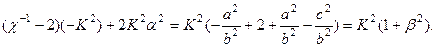
Тогда выражения для напряжений на границе примут вид:

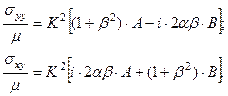(4.8.6)

Подстановка выражений (4.8.6) в граничные условия (4.84), после упрощений, дает систему уравнений для определения амплитудА, В:

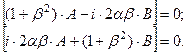(4.8.7)

Поскольку система (4.8.7) однородна, она имеет ненулевое решение только в том случае, когда ее определитель равен нулю. Это условие дает уравнение для определения скорости распространения искомых волн: 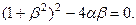(4.8.8)

Уравнение (4.8.8) называется уравнением Рэлея, а искомая скорость скоростью поверхностных волн Рэлея. Для ее определения получается алгебраическое уравнение. Введем переменную , тогда

.

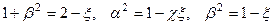Учитывая это, уравнение (8) после простых преобразований принимает вид 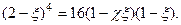, после приведения подобных членов, получим:

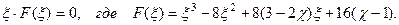(4.8.9)

Отбрасывая посторонний корень 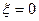,получаем уравнение для определения нужного корня в интервале :

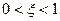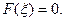(4.8.10)

Исследуем уравнение на предмет наличия нужного корня. Для этого определим знаки многочлена на концах промежутка, т.е. при и . Несложные подсчеты дают . Поскольку функция непрерывна и меняет свой знак, то отсюда следует, что хотя бы один корень на данном интервале есть.