Причем, единственными отличными от нуля компонентами тензора напряжений, в этом случае являются

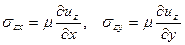. (4.9.3)

Будем искать решение в виде волны, бегущей по направлению оси 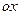с неизвестной и подлежащей определению скоростью :

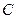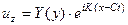. (4.9.4)

Подстановка (4.9.4) в уравнение (4.9.2) приводит к следующему уравнению относительно неизвестной функции :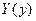

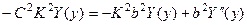, которое можно привести к виду

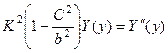. (4.9.5)

Уравнение (4.9.5) , в зависимости от соотношения между скоростью искомой волны и скоростью поперечных волн в среде, допускает решения разного характера. Если искомая скорость меньше скорости поперечных волн, решением уравнения (4.9.5) будут экспоненты

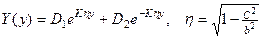. (4.9.6)

Если искомая скорость больше скорости поперечных волн, решение уравнения (4.9.5) будет иметь форму

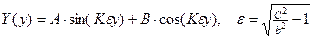. (4.9.7)

При наших предположениях о характере искомой волны решение для полупространства необходимо брать в виде (4.9.6) из требования убывания возмущений с глубиной, причем постоянная должна быть тождественно равна нулю.

Поэтому будем искать решение в виде (4.9.7) для слоя 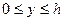и в виде (4.9.6) для упругого основания:

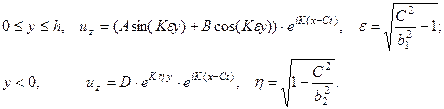(4.9.8)

Это означает, что искомая скорость волн должна удовлетворять неравенствам 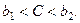(4.9.9)

Непрерывность перемещения 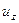и единственной отличной от нуля компоненты вектора напряжений 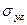на границе 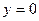,с учетом (4.9.3), (4.9.8), дает два уравнения 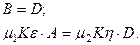(4.9.10)