На свободной поверхности упругого слоя должна быть равна нулю компонента вектора напряжений , что приводит к условию
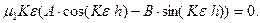 (4.9.11)
(4.9.11)
Уравнения (4.9.10), (4.9.11), после исключения амплитуды 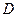 и простых упрощений, приводят к следующей системе двух уравнений для определения
и простых упрощений, приводят к следующей системе двух уравнений для определения 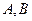 :
:
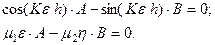 (4.9.12)
(4.9.12)
Поскольку мы ищем нетривиальное решение, определитель системы должен быть равным нулю. Это условие дает дисперсионное уравнение, позволяющее определить скорость волн в зависимости от их длины:
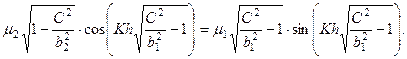 (4.9.13)
(4.9.13)
Для исследования решения этого уравнения введем вспомогательные обозначения: 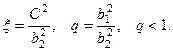 (4.9.14)
(4.9.14)
По условиям (4.9.9) нашей задачи искомая величина 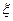 должна находится на интервале
должна находится на интервале 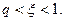 (4.9.15)
(4.9.15)
Учитывая введенные обозначения, перепишем уравнение (4.9.13) в более удобной для исследования форме. При этом с одной стороны уравнения сосредоточим тригонометрические функции, с другой чисто иррациональные функции.
Тогда уравнение (4.9.13) примет следующий вид:
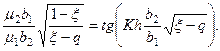 (4.9.16)
(4.9.16)
Полученное уравнение очень легко поддается графическому анализу на промежутке (4.9.15). Действительно, даже в самой неблагоприятной ситуации, когда максимальное значение аргумента тангенса при 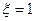 меньше
меньше 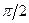 , т.е.
, т.е. 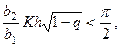 (4.9.17)
(4.9.17)
Тангенс непрерывно изменяется от нуля на левой границе промежутка (4.9.15) до некоторого заведомо положительного значения на правой границе области. При этом функция, стоящая в левой части уравнения (4.9.16), от бесконечно больших значений на левой границе непрерывно меняется до нуля на правой границе. Это позволяет сделать вывод о том, что хотя бы один корень уравнения (4.9.16) на требуемом интервале есть всегда.
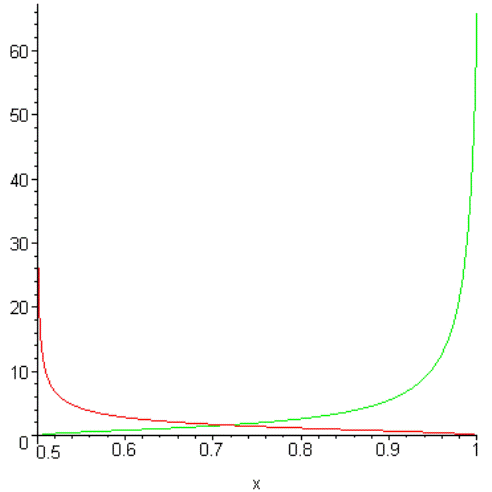
Рис.4.10 Иллюстрация графического исследования при определении скорости волн Лява.
Обратим внимание, что физически условие (4.9.17) означает или большую, по сравнению с толщиной слоя, длину волны или, при фиксированной длине волны, малую по сравнению с ней толщину слоя. Это следует из того, что где длина волны.
С увеличением максимального значения аргумента тангенса число корней уравнения (4.9.16) возрастает. Это означает, что для данного значения длины волны существует дискретный набор значений скоростей. Поскольку 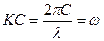 , большим скоростям волны соответствуют большие частоты. Для волн всех типов и физической природы известно, что волны с большей частотой затухают быстрее при распространении в реальных средах, где всегда есть диссипация энергии. Это приводит к тому, что в реальных средах очень быстро остаются только те волны, для которых частота меньше. Поэтому реализуется на практике меньшая из дискретного набора скорость волн с данной длиной. На рис.4.10 приведена иллюстрация графического исследования волн Лява для следующих значений безразмерных параметров задачи:
, большим скоростям волны соответствуют большие частоты. Для волн всех типов и физической природы известно, что волны с большей частотой затухают быстрее при распространении в реальных средах, где всегда есть диссипация энергии. Это приводит к тому, что в реальных средах очень быстро остаются только те волны, для которых частота меньше. Поэтому реализуется на практике меньшая из дискретного набора скорость волн с данной длиной. На рис.4.10 приведена иллюстрация графического исследования волн Лява для следующих значений безразмерных параметров задачи: 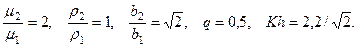
Как и следовало ожидать, скорость волн Лява зависит от длины волны. Это означает, что в отличие от волн Рэлея, волны Лява имеют дисперсию и волновой пакет будет со временем изменяться.
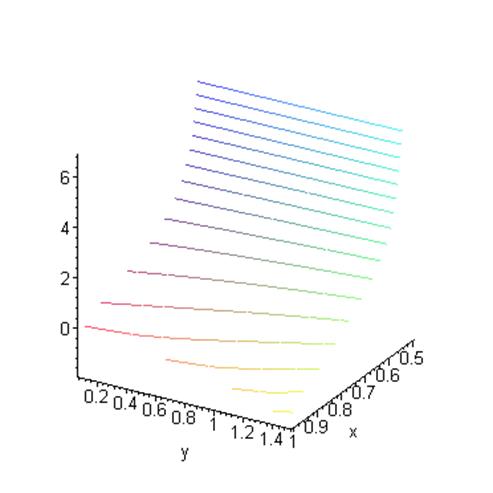
Рис.4.11. Трехмерный график линий уровня функции Лява в зависимости от переменных и Нулевая линия уровня соответствует скорости волн Лява в зависимости от длины волны.
Еще одна особенность волн Лява, а именно дискретный набор характерен для волноводов, в которых распространяется однотипная волна. Рассмотрим распространение в пластине волны с поперечной поляризацией, которая распространяется, многократно отражаясь от стенок пластины, которые жестко закреплены. Пусть падающая волна имеет волновой вектор с координатами 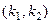 ,а отраженная волна –
,а отраженная волна – 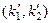 (рис.4.12). Тогда решение в выбранной системе координат можно искать в виде
(рис.4.12). Тогда решение в выбранной системе координат можно искать в виде 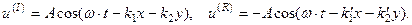
Дата добавления: 2015-12-29; просмотров: 837;
