Для того чтобы результирующее колебание

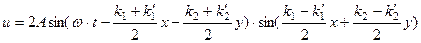
обращалось в нуль во всех точках плоскости 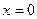необходимо, чтобы 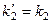, а из сохранения волнового числа 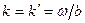следует равенство 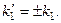К значению не равному тождественному нулю приводит, только равенство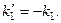

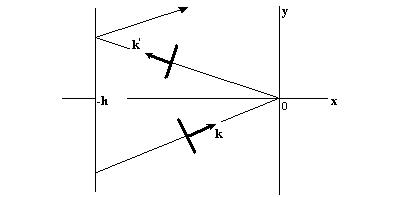
Рис.4.12 Волны в волноводе в виде пластины (–h < x < 0).

Используя полученные результаты можно переписать решение в виде:

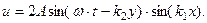
Для того, чтобы удовлетворить граничному условию 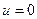и на второй границе 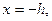должно быть выполнено условие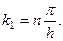

Интересно отметить, что групповая скорость таких волн

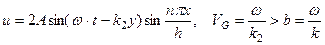
Больше скорости волн в безграничном пространстве. Волновой вектор волны в волноводе связан с волновым вектором волны в свободном пространстве зависимостью

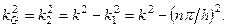
Отсюда следует, что существует максимальная длина волны, соответствующая минимальному волновому числу 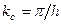. Волны с длиной большей 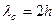распространяться в волноводе не могут. Одновременно можно сказать, что волны с частотой меньшей предельной 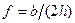также не могут распространяться в данном волноводе. Длина, соответствующая критической, называется длиной волны отсечки.