Сұйықтықтың тегіс және қисық сызықты беттерге түсіретін қысымы.

Денеге әсер ететін толық гидростатикалық қысымның күші, сол дененің ауданының гидростатикалық қысымның ауылық центріндегі абсолюттік шамасына көбейтіндісіне тең.

Ашық резервуарда, 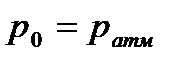болғанда, тегіс жұқа денеге әсер ететін толық гидростатикалық қысым күші, дененің ауданын артылған гидростатикалық қысымға көбейтіндісіне тең.

Қысым центрі деп артылған қысымның түскен нүктесіндегі қысымды атайды .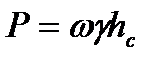

Архимед заңы, была айтылады: сұйықтыққа батырылған дененің жоғалтқан салмағы ығыстырылып шыққан сұйықтықтың салмағына тең. Архимед заңы, сұйықтыққа толық емес батырылған денелерге де қатысты.

Ұсынылатын әдебиет

1. Б. Т. Емцев. Техническая гидромеханика М.: Машиностроение, 1987.

2. В.Г. Гейер и др. Гидравлика и гидропривод. М.:Недра, 1991.

3. Р. Р. Чугаев. Гидравлика. Ленинград: Энергия, 1975.

4. В.А. Кудинов, Э.М. Карташов. Гидравлика. М.: Высшая школа, 2007.

5. Механика жидкости и газа. /под ред. Швыдкого В.С. - М.: Академкнига, 2003.

СӨЖ-ге арнлаған бақылау сұрақтары:

1. Сұйықтықтың берілген тереңдіктегі гидростатикалық қысымның анықтамасы.

2. Сұйықтықтың ыдыс түбіне түсіретін қысымы.

3. Ыдыстың қисық сызықты қабырғаларына сұйықтықтыңтүсіретін қысымы.

4. Вакуумның және сұйықтықтың артылған қысымының анықтамалары.

3 Тақырып. Сұйықтық пен газдардың кинематикасы (3/1/1/1 сағ)

Дәріс жоспары

1. Сұйықтықтың қозғалыс түрінің классификациясы.

2. Қозғалыстағы сұйықтықтың екпіндік моделі.

3. Коши-Гельмгольц теоремасы.

4. Екпінді сызықтар және құбырлар. Екпінді құбырлар қасиеті.

5. Жылдамдықтың циркуляциясы туралы түсінік, Стокса және Томсона теоремалары.

6. Потенцияал қозғалыс жайындағы ұғым және оның сипаттамасы.

Дәрістің қысқаша мазмұны

Қалыптасқан қозғалыс деп сұйықтықтың, уақыт өтуімене бірге ағын жылдамдығы және қысымы барлық нүктелерінде өгермей,оның тек ағын ішіндегі бағытына байланысты болатын жағдайды атайды, яғни оның координаталарының функциясы болып табылады. Қалыптасқан қозғалыстың мысалы ретінде сұйықтықтың үлкен ыдыстытың тетігінен ағуын келтіруге болады.

Қалыптаспаған қозғалыс деп уақыт өтуімен берілген нүктедегі қозғалыс жылдамыдығы және қысым өзегріптұратын қозғалысты айтады, яғни Тек координаттың ғана емес сондай-ақ уақыт функциясы болып табылады. Қалыптаспаған қозғалыстың мысалы ретінде улкен ыдыстан айнымалы ықпалмен ағып турған суйықтықтың ағуын келтіруге болады.

Ағын түзуі,берілген уақытта барлық нүктелердегі жылдамдық векторы оған (түзуге) жанама болатындай сипатталады.

Элементар ағын. Егер қозғалыстағы сұйықтықтан шексіз кішкентай тұйық контур жүргізілетін болса және оның барлық нүктелері арқылы ағын түзуін өткізсек онда берілген уақытқа сәйкес құбыр тәріздес өткізбейтін бет пайда болады, ол ағын құбыры деп аталады.

Ағын. Үздіксіз бөлшектер массасын құрайтын қандайда бір бағытпен қозғалатын элементар ағындардың жиынтығы сұйықтықтың ағынын құрайды. Ағын толық немесе ішінара қатты қатты қабырғалармен шектелуі мүмкін, мысалықұбырда немесе арнада, және еркін болуы мүмкін, мысалыгидромонитордың аузынан шығатын ағын.

Ағынның қимасы. S ағынның оның бағытына перпендикуляр көлденең қимасын атайды.

Ағынның шығыны. Q бірлік уақытында ағынның қимасы арқылы өтетін сұйықтықтың көлемі. Сұйықтық көлемім³/с немесе л/с өлшенеді.

Сұйықтандырылған периметр χ сұйықтық қабырғалармен жанасатын ағын қимасының бөлігі.

Гидравликалық радиус R ол – ағын қимасының аумағының сұйықтандарыған периметрге қатынасы:

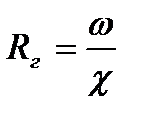(3.1)

Ағынның орташа жылдамдығы 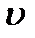ол – ағын шығының ағын қимасына қатынасы, яғни:

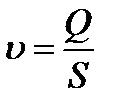(3.2)

Біртекті деп ағын қимасы және ағынның орташа жылдамдығы ұзындығы бойынша өзгермейтін сұйықтықтың қалыптасқан қозғалысын атайды. Біртекті қозғалысының мысалы ретінде сұйықтықтың цилиндрі тәрізді құбыр ішінде немесе қимасы және тереңдігі тұрақты арндағы қозғалысы.

Біртекті емес ұзындығы бойынша өзеретін ағын қимасы және орташа ағын жылдамдығы ұзындығы бойынша өзгермейтін сұйықтықтың қалыптасқан қозғалысы. Біртекті емес қозғалыстың мысалы ретінде сұйықтықтың конус тәріздес құбырдағы, табиғи арнада, деңгейлер айырымындағы қозғалысы.

Екпінді ағын деп бүкіл ағын қимасының апериметірінің барлық нүктесінде сұйықтық қатты қабырғамен жанасатын ағынды атайды. Екпінді ағынның мысалы ретінде су құбырларындағы сүдың қозғалысы аталады. Екпінді ағынның мысалы ретінде су құбырындағы судың қозғалысын келтіруге болады.

Екпінсіз ағын деп еркін бетке ие ағынды атайды. Екпінсіз ағын мысалы ретінде өзендегі, арналардағы, канализациядағы судың ағынын атауға болады.

Егер қатты дене айналмалы немесе ілгермелі немесе айнлмалы ілгермелі қозғала алатын болса, сонымен қатар өзінің пішінін сақтаса 3 а) суреті, онда оған қарағанда бөлшек айнала қозғалғанда деформациялануы да мүмкін 3 б) суреті. Сұйық бөлшектердің осы мүмкін қозғалыстары берілген қозғалыстар өрісінің сипаттамасына тәуелді болады.Жалпы жағдайда сұйық бөлшек осы үш қозғалыстың барлығын жасап шығады 3 в) суреті, сондықтан сұйық бөлшектің қозғалысын ілгермелі, айнымалы және деформацияланған деп жіктеуге болады – Коши – Гельмгольц теоремасы.

Теория жүзінде сұйықтық қозғалысын екі топқа бөлуге болады: аналмалы қозғалыс, әдетте оны қйынды деп атайды, және айналмалы емес, оны құйынсыз деп атайды.

Суйықтықтың элементар көлемінің бұрыштық жылдамдығын – құйын деп аталады, ал құйынның векторының кез-келген нүктесіндегі жанамасы – құйынды түзу деп атайды.

Элементар тұйық контурдың барлық нүктелері арқылы жүргізілген, құйынды сызықтардың арқасында пайда болған бетті құйынды түтік деп атайды, ал құйынды трубканың ішіне қамалған сұйықтық – құйынды жіп- арқан деп аталады.

Қозғалыстың негізгі кинематикалық сипаттамасын қозғалыс векторының бұрыштық жылдамдығы деп аталады, координаттық осьтерге проекциясымен анықталады:

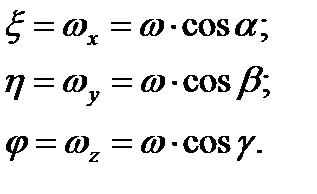(3.3)

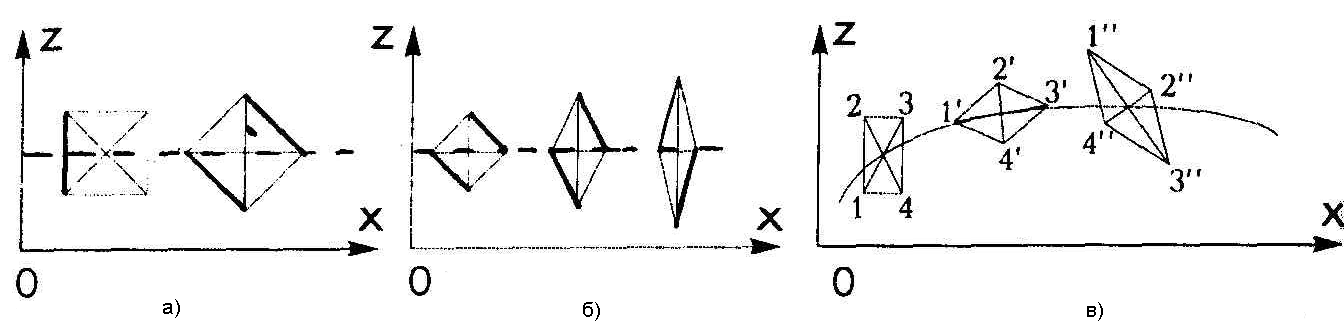
3.1 сурет – Құйынды және құйынсыз қозғалыстың кинематикалық сипаттамасы.

Осы проекциялар ξ, η и φ құйынның компоненттері деп аталады. Құйын компоненттерінің теңдеулер жуйесі (3.4) көрсетілген. Әдетте құйын деп екеселенген жылдамдықты атайды 2ω, бірақ басқа да аталуы да болады, яғни құйын деп кәдімгі бұрыштық жылдамдықты атауға болады.

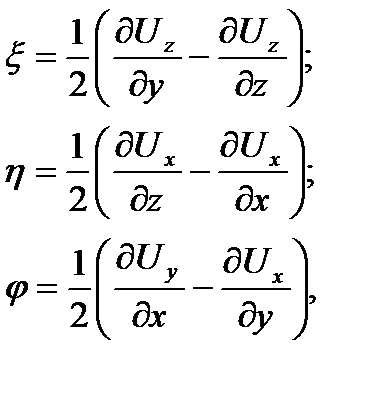3.4)

мұндағы U_x, U_y, U_z – орын бөлшектің аустыру жылдамдығының проекциялары сәйкесінше X, Y, Z осьтеріне.

Құйынсыз қозғалыс – құйын нөлге тең болатын қозғалыс яғни бұрыштық жылдамдық ω = 0. Ол құйынның бүкіл компонентерінің теңдігін талап етеді: ξ = η = φ = 0. (3.4) теңдеулер жүйесін ескере отырып келесі анлитикалық шарттар қажет:

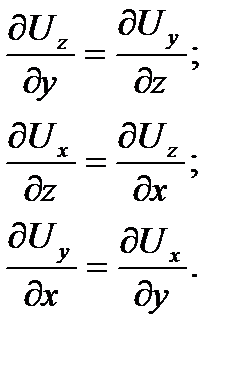(3.5)

(3.5) құйынсыз қозғалыстың аналитикалық шарты (3.5) жылдамдық потенциалы деп аталатын φ(x, y, z, t) ерекше функциясының координатының бар екенін көрсетеді, оның дербес туындылары сол координаттармен жылдамдық компонетттерін анықтайды яғни:

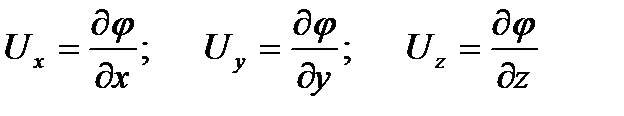. (3.6)

Осындай функция шыныда да бар (3.5), оны U_x, U_y и U_z мәндерін қою арқылы оңай көруге болады (3.6) және (3.5). Қарастырылған функцияның енгізілген аталуына байланысты φ (жылдамдық потенциалы) құйынсыз қозғалыс потенциалды деп аталады.

Құйынды қозғалыстардың арасында жеке түрі бұрғылы қозғалысы бар, сол нүктедегі бұрыштық жылдамдықтың векторы сызықтық жылдамдықтың векторымен сәйкес келетін кезі.

Гидромеханикада кеңінен «жылдамдық циркуляцисяы» деген ұғымы қолданылады – сұйықтық немесе газ ағынының кинематикалық сипаттамасы, құйындалу мөлшері ретінде қолданылад.

Тұйық контурдың бойымен жылдамдықтың циркуляциясы қисық сызықты интегралмен сипаттталады: 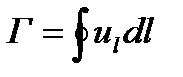, мұнда u_l – сұйықтық немесе газдың контурдың кез-келген нүктесіндегі сол контурға жанамасына проекциясы; dl – қарастырылып отырған нүктені ескере отырып, контурдың ұзындығының элементі.

Гельмгольц теоремасына сәйкес – құйынды жіптер кенеттен аяқталуы мүмкін емес: олар не шексіздікке дейін созылады, не сақинаға айналады, не қатты денемен шектеледі.

Ұсынылатын әдебиет

1. Б. Т. Емцев. Техническая гидромеханика М.: Машиностроение, 1987.

2. В.Г. Гейер и др. Гидравлика и гидропривод. М.: Недра, 1991.

3. Р. Р. Чугаев. Гидравлика. Ленинград: Энергия, 1975.

4. В.А. Кудинов, Э.М. Карташов. Гидравлика. М.: Высшая школа, 2007.

5. Механика жидкости и газа. /Под ред. Швыдкого В.С. - М.: Академкнига, 2003.

СӨЖ-ге арналған бақылау сұрақтары:

1. Сұйықтандыру периметрінің және гидравликалық радиусының аықтамасы.

2. Коши-Гельмгольца теоремасын шығару.

3. Стокса и Томсона теоремасын шығару.

4 Тақырып. Сұйықтық пен газдың қозғалысының негізгі теңдеулері (4/2/1/1 сағ)

Дәрістің жоспары

1. Шығынның, үздіксіздіктің теңдеулері, Бернулли және элементар ағынның және біртекті ағынның қозғалыс мөлшері.

2. Үздіксіздіктің дифференциалды теңдеуі. Идеал және тұтқырлы сұйықтықтың дифференциалды қозғалыс теңдеуі.

3. Орташаландырылған турбулентті ағынның қозғалысының тендеуі. (Рейнольдса теңдеулері)

4. Ұқсастық теорисының негіздері.

Дәрістің қысқаша мазмұны

Ағынның үздіксіздік теңдеуі

Q₁= Q₂= Q=const. (4.1)

Сұйықтықтың көлемдік шығыны 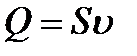(шығын теңдеуі) болғандықтан, газдың массалық шығыны 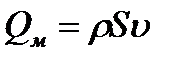, онда (4.1) теңдеуі келесі түрде жазылуы мүмкін:

- тамшылы сұйықтық үшін 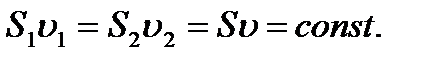(4.2)

- газ тәріздес сұйықтық үшін 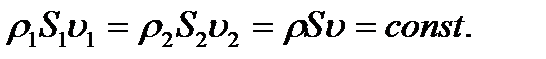(4.3)

Тұтқырлы сұйықтықтың барлық қималары үшін келесіні жазуға болады:

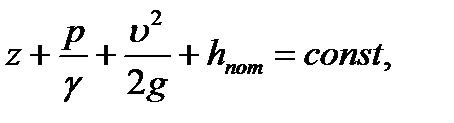(4.5)

мұнда z – салыстыру бетінен қиманың ауырлық центріне дейінгі қашықтық;

p – Осы қиманың ауырлық центрінің ортасындағы қысым;

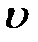- осы қиманың ортасындағы орташа жылдамдығы;

h_пот – меншікті энергия.

Ағынның кез-келген нүктесіндегі меншікті энергия (4.1 сурет):

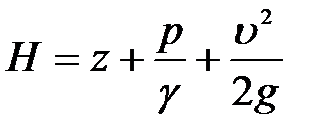
(4.5) теңдеуі Бернулли теңдеуі деп аталады.

Бернулли теңдеуінің барлық мүшелері сызықтық өлшемділігі бар, сондықтан олардың әрқайсысы биіктік деп аталады.

Бернули теңдеуінің геометриялық мағынасы былай пайымдаға болады: сұйықтықтың қалыптасқан қозғалысы кезінде төрт биіктіктің соммасы (қалып, пьезометриялық, екпінге сәйкес келетін биіктіктер, екпіннің жоғалуына сай келетін биіктіктер) ағынның бойында өзгермейді.

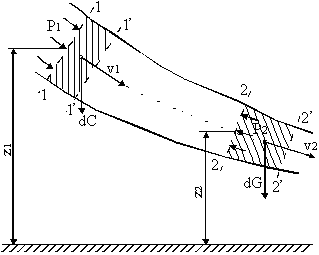
4.1 Сурет – сұйықтықтың және газдың теңдеуін шығаруға байланысты

Қозғалыс мөлшерінің гидравликалық теңдеуі немесе секундтық қозғалыс мөлшерінің теңдеуі: ағында бөлінген бір беттен 1-1 басқа 2-2 бетке өту кезіндесыртқы кез-келген оське проекция:

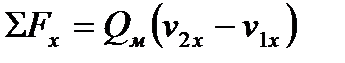(4.6)

Реалды сұйықтықтар бір бөлшекткердің екіншісіне қарағандағы ығысуына қарсы тұратыны белгілі. Ньютонның пайымдауы бойынша, ығысуға қарсы кедергі күші және Кулон күштеріне қарама-қарсы, қысымға тәуелсіз, бірақ ығысу болған ауданға тәуелді және ығысу жылдамдығына тәуелді. Ол Ньютона заңы деп аталады:

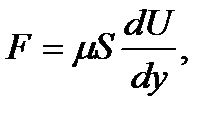
мұнда F – кедергі күші, S –ығысу ауданы, dU/dy – ағын бағыта қарай нормальдің жылдамдқ градиенті.

Кедергі күштерін ескере отырып, Ньютон заңы жалпы дифференциалды теңдеуді құрастыруға мүмкіндік береді, оны біз тұтқырлық күштері деп атаймыз. Тұтқырлық күштерін шартты түрде көлемді күштерге айналдырамыз және сол күштердің үдеуін келесіде қалыптастырамыз:

.

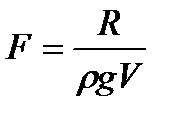Тұтқырлық күштерінің проекцияларын сәйкесінше F_x, F_y, F_z, жәнеЭйлера теңдеуіне енгіземіз (2.1). Сонда

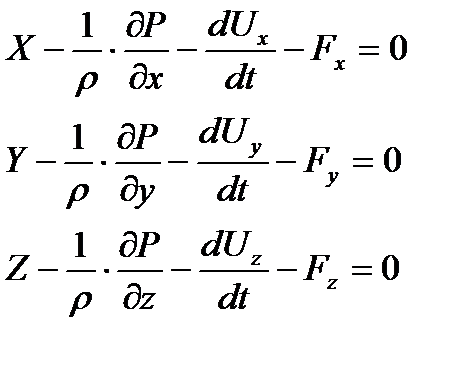(4.7)

Тұтқырлық күші үш кернеу түрінде болады: – нормальді (сығылу және ашылу кернеуі) және екі жанама. Осы кернеулер түрлі бағыттарда әсер етеді.

Навье-Стокса теңдуін түрлендіру арқасында аламыз, олар қозғалатын орталар үшін Ньютонның екінші заңының түсінірілуі болады:

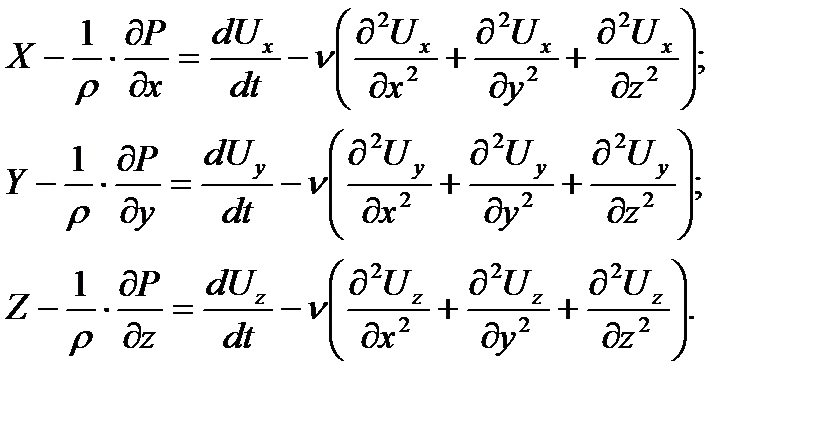(4.8)

Навье-Стокс теңдеуі ламинарлы және турбулентті ағындарға қолданылады. Бірақ берілген шекаралық шарттарда кинематикалық сипаттамалардың пульсациялануының кездесоқ болуы, турбулентті ағынның күрделілігін көрсетеді.

Тұтқырлығы тұрақты сығылмайтын сұйықтықтың қозғалыс теңдеуіне ортаның мезеттік жылдамдықтың мәнін қойып 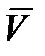орташаланған мәнінің соммасына тең және пульсациялану 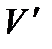құраушысына координаттардың бағытына қарай қоып көрейік

,

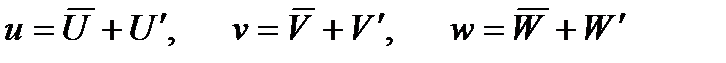Турбулентті ағындатек жылдамдық қана пульсацияланбайтынын ескереміз. Сонда Навье-Стокса қозғалыс теңдеуінің орнына Х осіне проекциясын аламыз:

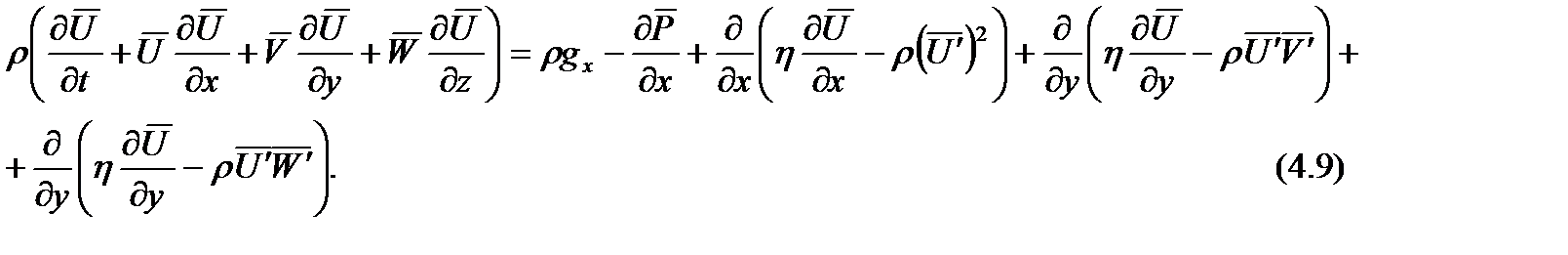
Осындай теңдеулер барлық координаталарға тән. Осыдай типті теңдеулерді Рейнольдсатеңдеулері деп аталады. Турбулентті ағындарға арнайы жазылған қозғалыс теңдеулері Навье-Стокс теңдеулерінен айырмашылығы айқын көрінеді.