Састық теориясының негіздері

Ағындардың геометриялық ұқсастығының шарттары ол, олардың сызықтық мөлшерлерінің және аудандары мен көлемдерінің арасындағы айырмашылық:

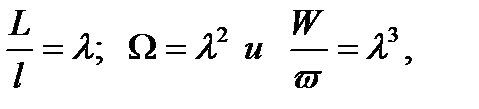(4.7)

мұнда 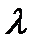- модельдеудің сызықтық масштабы.

Кинематикалық ұқсастықтың қатынастары үшін, геометриялық ұқсастықтан басқа, келеси қатынастың орыдалуы мақсат:

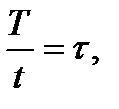(4.8)

мұнда 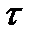- уақытты модельдеу масштабы.

Ағынның динамсикалық ұқсастығының шарты, ағындардың сұйықтықтарынынң тығыздығының тұрақтылығы, оның кинематикалық ұқсастығына қарағанда басты болады:

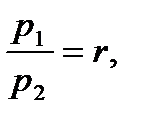(4.9)

мұнда p₁ и p₂ – бірінші және екінші сұйықтық ағынының тығыздығы.;

r – тығыздықтың модельдеу масштабы.

Ұсынылатын әдебиет

1. Б. Т. Емцев. Техническая гидромеханика М.: Машиностроение, 1987.

2. В.Г. Гейер и др. Гидравлика и гидропривод. М.:Недра, 1991.

3. Р. Р. Чугаев. Гидравлика. Ленинград: Энергия, 1975.

4. В.А. Кудинов, Э.М. Карташов. Гидравлика. М.: Высшая школа, 2007.

СӨЖ-ге арнайы бақылау сұрақтары

1. Қубыржолдағы сұйықтықтың шығынын есептеу.

2. Реал сұйықтықтардың ағыны үшін Бернули теңдеуін шығару. Құбырдағы екпінді анықтау. Сұйықтықтың жылдамдығын, қысымын анықтау.

3. Толық және пьезометрлік екпіндердің графикалық кескіні.

4. Қозлғалыс мөлшерінің гидравликаық теңдеуін есептеу.

5. Ұқсастық шарты.

5 Тақырып. Құбырдағы сұйықтықтың қозғалысы және құбыржолдарды гидравликалық есептеу (4/2/1/1сағат)

Дәріс жоспары

1 Ұзындық бойынша екпіннің жоғалуы. Гидравликалық кедергі коэффициенті

2. Жергілікті екпіннің жоғалуы. Эквивалентті ұзындық туралы ұғым.

3. Сұйықтық қозғалысының режимі.

4. Гидравликалық тегіс және тегіс емес құбырлар туралы түсінік.

5. Құбырлардағы гидравликалық соққы

6. Құбыржолдардың классификациясы

7. Қарапайым қубыржолдардың негізгі есептері

8. Айырылған және паралель құбыржолдарын есептеу.

9. Сұйықтықты сорғышпен тарту құбыржолдары. Құбыржолдардың екпінді сипаттамасы.

10. Қысымның улкен ауытқуы кезіндегі газ құбыржолдарын есепте.

Дәрістің қысқаша мазмұны

Екпінннің (энергияның) жоғалуы кедергінің екі түрінің арқасында болады:

1)үйкеліс күшімен сипатталатын, ұзындығы бойынша кедергі;

2)ағынның молшері және жылдамдығының өзгеруі арқасында пайда болатын жергілікті кедергі.

Екпіннің құбыр ұзындығы бойынша жоғалуы әдеттеДарси-Вейсбах формулысымен анықталады:

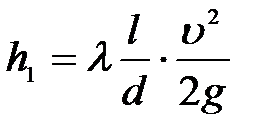(5.1)

Ал жергіліктісі Вейсбаха формуласымен есептеледі

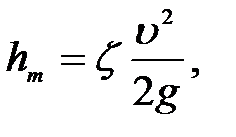(5.2)

мұнда 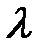- гидравликалық үйкеліс коэффициенті (Дарси коэффициенті);

l – құбыржол ұзындығы;

d – құбыржол диаметрі;

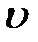- ағынның орташа жылдамдығы;

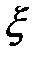- жергілікті кедергі коэффициенті.

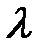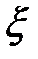и коэффициенттері өлшемсіз. Тәжірибелік зерттеулер осы коэффициенттер көптеген факторларға тәуелді екенін көрсеті, қозғалыс режимі және қабырғалардың тегіс болмау.

Сұйықтықтың жылдамдық режимі.Құбырдағы сұйықтық екі режиммен сипатталуы мүмкін: 1) ламинарлы және 2) турбулентты.

Оны анықтау үшін өлшемсіз парамер Re бар (Рейнольдс саны):

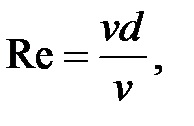(5.3)

мұнда v – тұтқырлықтың кинематикалық коэффициенті.

Ламинарлы режим турбулентіге өтетін Рейнольдс санын Сындық деп атайды. Рейнольдса тәжірибесі бойынша Re_кр=2320. Егер Re<2320 он сұйықтықтың қозғалысы ламинарлы режимде өтеді, ал Re>2320 болса турбулентті режимге жатады. Рейнольдстың сындық санына сәйкес келетін жылдамдықты сныдық жылдамдық деп атайды:

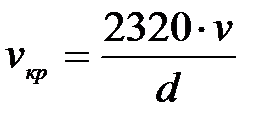(5.4)

Сұйықтықтың екпінсіз ағыны кезінде Рейнольдс санын келесі формуламен анықтайды:

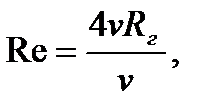(5.5)

мұндаR_г – гидравликалық радиус. Бұл қозғалыста Re_кр=580.

Гидравликалық соққы әдетте қысымның кенет көтерілуін атайды, сұйықтықтың ағынын кенет тоқтатқан кезде пайдаболатын, екпінді құбыр жолда пайда болады. Дәлірек айтсақ, гидравликалық соққы, жылдамдықты кенеттен өзгерту салдарынан пайда болатын, тамшылы сұйықтықтың серппелі құбыржолдың ішінде болатын тербелмелі процесс. Осы процес өте тез өтеді, жәнекенеттен қысымның жоғарлаумен төмендуімен сипатталады. Қысымның өзгеруі тікелей құбыржол қабырғалары мен сұықтықтың серппелі деформациясына байланысты.

Кәдімгі құбыржолды есептеу. Екпіннің жалпы жоғалуы ұзындығы және жергілікті жоғалулардан құралады. Осы шамаларының қатынастарына қарай ұзын, қысқа және қарапайым күрделі құбыржолдарды айырады.

1.1 сурет – Қарапайым құбыржолдың кескіні

1—1 и 2—2 Қималары үшін Бернули теңдеуін жазайық. a₁=a₂ және жылдамдық екпіндерін ескермей, мынаны аламыз

немсе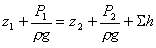

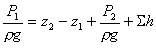
Бірінші екі қосындының соммасы Dz+ P₂/(rg) статистикалық екпін, және оны қайсы бір сұйықтықтың көтерілуінің эквивалентті геометриалық биіктігі ретінде қарастыруға болады Н_ст, ал соңғы Sh қосындысын— шығынның дәрежелік функциясы ретінде, сонда

Н_потр= Н_ст+Sh= Н_ст+KQ^m, (5.8)

мұнда К шамасы, құбыржол кедергісі деп аталады, және m көрсеткіші ағу режиміне қарай әр-түрлі мәні бар.

Ламинар ағын үшін жергілікті ағындарды эквивалентті ұзындықпен алмастырғанда:

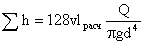
Сондықтан,

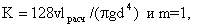(5.9)

мұнда l_расч=l+l_экв.

Турбулентті ағын үшін жылдамдықты шығын арқылы өрнектей отырып:

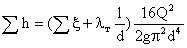
одан,

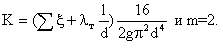(5.10)

Жалғасатын бір жіпке жалғастырылған құбыр жолдар арқылы сұйықтықтың әр-түрлі диаметрлер арқылы өту процессын айтады. Мұнда, екпіннің жоғалуының жалпы мәнән, әрбір нүктедегі екпіннің жоғалуының қосындысы арқылы анқтайды:Sh_M-N = Sh₁ + Sh₂ + Sh₃. , гдеSh₁, Sh₂,Sh₃ 1, 2, 3, …, n-ші аймақтағы екпіннің жоғалуы.

Параллель қосу кезінде керісінше болады.

Q₁ + Q₂+ Q₃ = Q;

Sh₁ = Sh₂= Sh₃.

Айырылған жалғау. Бірнеше қарапайым құбыржолдардық қосындысы. Мұнда

Q₁ + Q₂+ Q₃ = Q;

Н_М=Н_ст1+K₁Q₁^m.

Н_М=Н_ст2+K₂Q₂^m;

Н_М=Н_ст3+K₃Q₃^m.

Центрден тепкіш, соратын және екпінді құбыржолдары бар сорғыш қондырғысының схемасын қарастырайық (5.2 суреті). Екпінді құбыржол ол сорғыштан резервуарға жүргізілген құбыр жүйесі. Сорғыш қондырғысы, суды ашық резервуарға береді, сол суды ол Q шығыны және Н_г арқылы көтеруі қажет, одан басқа, согратын және екпінді құбырлардағы едергіні жеңуі қажет. Ол жағдайда пайдаланатын шығын Н_потр мынаған тең

Н_потр = Н_г + h_пот. (5.11)

Жалпы екпінді жоғалту

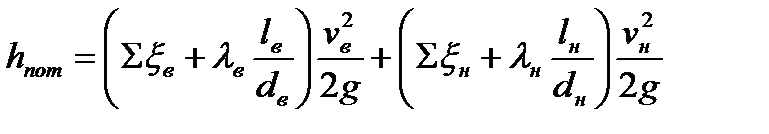, (5.12)

мұндаλ_в и λ_н- соратын және екпінді құбырдың гидравликалық үйкеліс коэффициенті; Σξ_в, Σξ_н – жергілікті кедергілердің коэффициенттерінің соммасы.; l_в и l_н - соратын және екпінді құбырдың ұзындығы; d_в и d_н – құбыржолдар диаметрі; v_в и v_н – құбыржолдардағы орташа жылдамдықтар.

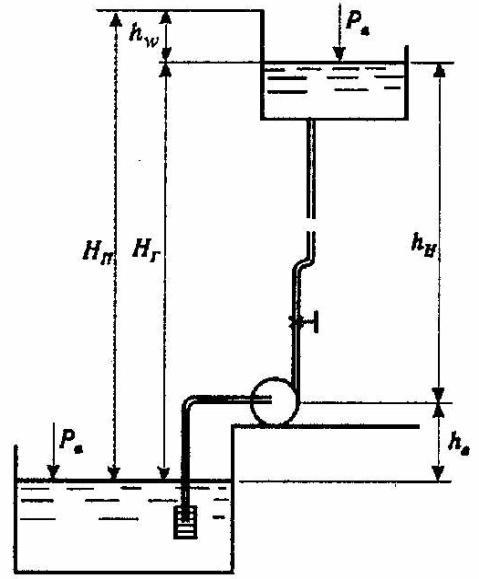
5.2 сурет – сорғыш қондырғысының кескіні

Соратын және екпінді құбырдың орташа жылдамдығы

; .

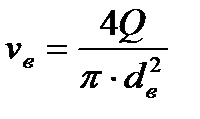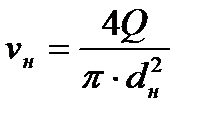(5.12) формуласына орташа жылдамдықтардың мәнән қоямыз, сонда екпіннің жоғалуы мынаған тең

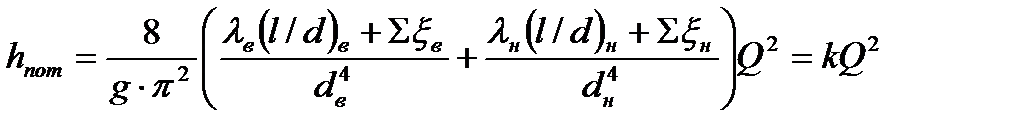. (5.13)

(5.13) формуласында k мәні сорғыш қондырғысының құбырларының кедергісі. Суды Н_г биіктігіне көтеруге қажетті екпін:

Н_потр = Н_г + kQ². (5.14)

Н_потр = f(Q) графикалық тәуелділігі қажетті екпін қисығы деп аталады (сорғыш қондырғысының сипаттамасы). Ол сорғыштың жұмыс істеу режимын анықтауға қажет.

Газ құбыржолдарын есептеудің негіздері.Тамшылы сұйықтықтардың қозғалысына қарағанда газдардың қозғалысында біраз айырмашылықтар бар.

Газдың меншікті энергиясының газқұбырының элементар юөлігіндегі өзгеруін, былай жазуға болад:

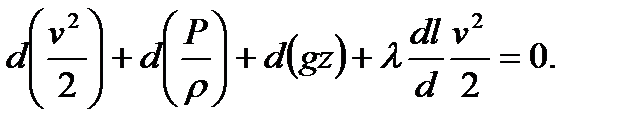
Осында қысымның меншікті энергиясынан әлдеқайда төмен меншікті кинетикалық және жағдай энергиясын ескермей, және элементар бөлік үшін ρ = const, қабылдай отырып аламыз.

.

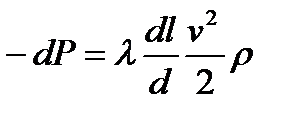Үздіксіздік теңдуіне сай газ үшін v = v₁ρ₁/ρ, онда

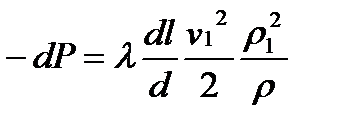. (5.15)

1 индексі газ құбыржолының басындағы газ параметрі, индекс 2 – құбыржолдың соңындағы параметрлер. Басқалары индексіз.

Изотермиялық процесс кезінде газ күйінің теңдеуіне сай мынаны жазуға болады: Р/ρ = Р₁/ρ₁; ρ – мәнін (5.15) теңдеуіне қойып, мынаны аламыз

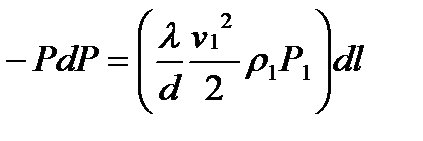. (5.16)

Жалпы түрде 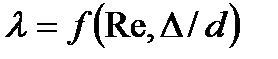, мұнда 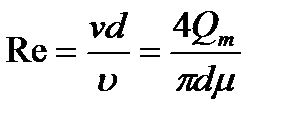. Берілген құбырға бірдей тегіссіздкті қабылдай отырып (Δ/d), және изотермиялық процесс кезінде температура тұрақты екенін ескеріп Дарси коэффициентін λ газ құбыржолының бойында тұрақты деп есептеуге болады. Онда (5.16) теңдеуін 0 ден l-ға дейін интегрлдау арқылыжәне Р₁–данР₂–ға дейін, мынаны аламыз:

,

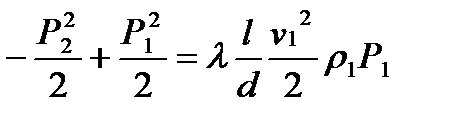Немесе келесі түрлендіру арқылы:

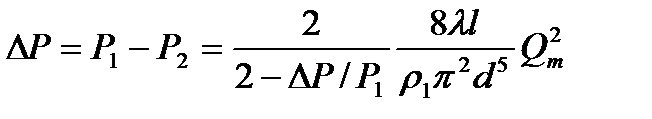. (5.17)

Газқбыржолдарын және ауа құбыржолдарын есептеу кезінде оның ішіндегі газ қозғалысының екі түрін ескерген жөн:

- онша үлкен емес өзгеріс .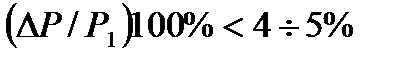

Онда практика үшін жеткілікті дәлдікпен 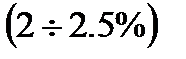, газ сығылуын ескермеуге болады, яғни оның қысымын 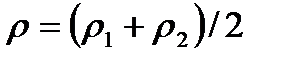=соnst деп және Дарси – Вейсбаха қарапайым формуласымен қолдануға болады;

- қысымның елерліктей өзгерісі кезінде 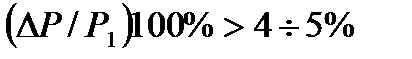. Онда сығылуды ескермеуге болмайды, және (5.17) формуласымен есептеу қажет.

Ұсынылатын әдебиет

1. Б. Т. Емцев. Техническая гидромеханика М.: Машиностроение, 1987.

2. В.Г. Гейер и др. Гидравлика и гидропривод. М.: Недра, 1991.

3. Р. Р. Чугаев. Гидравлика. Ленинград: Энергия, 1975.

4. В.А. Кудинов, Э.М. Карташов. Гидравлика. М.: Высшая школа, 2007.

СӨЖ-ге арнайы бақылау сұрақтары

1. Құбыржолдағы екпінді жоғалтуды анықтау.

2. Сұйықтықтың ағу режимін анықтау.

3. Гидравликалық кедергі коэффициентін анықтау.

4. Құбырдағы екпіннің жоғалуын анықтау.

5. Қажетті екпінін анықтау.

6 Тақырып. Сұйықтықтың тетіктер және ауздықтардан ағып шығуы (2/1/1/1 сағ)

Дәріс жоспары

1. Тұрақты екпіндегі жұқа қабырғадағы кішкентай тесік арқылы сұйықтықтың ағып шығуы.

2. Ағынның сығылуының түрлері.

3. Саптамалар арқылы сұйықтықтың ағып шығуы.

4. Лаваль шүмектері

Дәрістің қысқаша мазмұны

Тетіктікішкентай деп, егер оның өлшемі биіктігі бойынша ағын екпінінен аз болса 0,1 Н –на үлкен емес болады. Жұқа қабырға деп тетігінің қиырлары қайралған қабырғаны атайды, мұнда ағын тек жергілікті кедергіден өтеді.

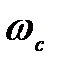сығылған қиманың ауданының тетік ауданына қатынасы сығылу коэффициенті деп аталады:

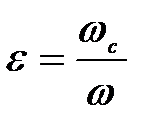(6.1)

Сипаттамасы бойынша сығылу толық болады, егер ағын тетіктің барлық периметірінің бойын сығылса, және толық емес, егер шетінен бір немесе бірнеше рет сығылатын болса.

Толық сығылу егер тетік шет қабырғалардан және ыдыстың түбінен жеткілікті қашықтықта болса мінсіз болады, және жетіксіз, егер оған қабырғалар мен ыдыстың түбінен әеср үлкен болса.

Тетіктен сұйықтықтың ағып шығу жылдамдығы:

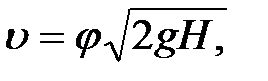(6.2)

мұнда 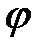- жылдамдық коэффициенті.

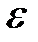сығылу коэффициенті және 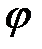жылдамдық коэффициентіні көбейтіндісі тетіктің шығын коэффициентідеп аталады ,

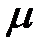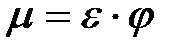(6.3)

Жұқа қабырғадағы тетіктен аққан сұйықтықтың шығыны келесі формуламен есептеледі:

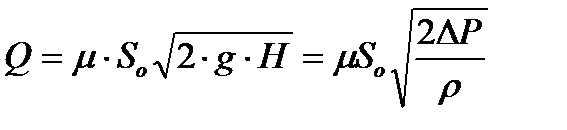(6.4)

Сатамалар деп қабырғасы жұқа тетікке кигізілген қысқа түтікті айтады. Саптаманың ұзындығы бес тетік диаметрінің үшеуіне тең.

Пішіні бойынша саптама: сыртқы цилиндр тәріздес, ішкіцилиндртәріздес, қиылысатын конус тәріздес, ажырайтын конус тәріздес және коноидальды болуы мүмкін.

6.1 суретінде екі шүмек көрсетілген, олар арқылы жоғарғы қысымдағы газдардың ағып шығу жүзеге асырылады; біріншісін кәдімгі конус тәріздес, ал екіншісін пішінді деп атайды. Артылған кинетикалық энергияны қысқа уақыт арасныда сығып оның атылып шығу процесы жүзеге асырылады. Бұл жағдайда газ бен қоршаған орта арасында соплолардың қабырғалары арқылы жылуалмасу процес өте аз болады, және газ температурасына онша әсер етпейді, ағу процессі адиабаталық процесске жақындайды.

Егер газ жылдамдығы дыбыс жылдамдығынан төмен болса, яғни М_* = u /с < 1, онда ағынды дыбысқа деінгі. Ал газ жылдамдығы дыбыс жылдмдығына тең болғанда (М_* = 1), сындық деп аталады. Газ жылдамдығының сындық жылдамдыққа қатынасы – газ қозғалысының жылдамдығының шарты деп атайды яғни λ = u/u_кр.

Жеткілікті қысымның арқасында газ қозғалысының жылдамдығы дыбыстың таралу жылдамдығынан жоғары болуы мүмкін.яғни М_* > 1 и λ > 1. Ол режимді дыбыс жылдамдығынан жоғарғы жылдамдық деп аталады.

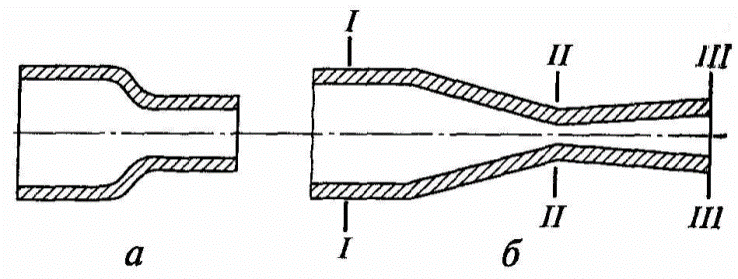
6.1 суреті – Конустәріздес (а) және пішінді (б) шүмектің кескіні

Жалпы жағдайды қарастырайық, - суретте көрсетілген газдың пішінді сопло арқылы ағуы 6.1, б. Газовый поток при переходе от начального сечения 1-1 Бастапқы қимадан II-II минималды қимасына газ ағыныны ақырындап жіңішкереді, II-II минималды қимасынан III- III қимасына ол біртекті кеңейуге ұшырайды. Сонымен осы соплода екі бөлікті бөліп шығаруға болады: жіңішкеру - конфузор және кеңейу - диффузор. Егер осындай соплонық ұзындық қимасы газдың дыбыс жылдамдығынан артық болып шығуына жол берсе, онда ол Лаваль шүмегі деп аталады.

Ұсынылатын әдебиет

1. Б. Т. Емцев. Техническая гидромеханика М.: Машиностроение, 1987.

2. В.Г. Гейер и др. Гидравлика и гидропривод. М.:Недра, 1991.

3. Р. Р. Чугаев. Гидравлика. Ленинград: Энергия, 1975.

4. В.А. Кудинов, Э.М. Карташов. Гидравлика. М.: Высшая школа, 2007.

СӨЖ-ге арнайы бақылау сұрақтары

1. Ағынның сығылу коэффициентін, жылдамдық коэффициентін, жергілікті кедергі коэффициентін, шығын коэффициентін анықтау.

2. Сұйықтықтың тетіктен ағып шықандағы шығынын анықтау.

3. Саптама арқылы сұйықтықтың шығынын анықтау.

7 тақырып. Қатты денені айналып өту. Шекаралық қабат (3/1/1/1 сағ)

Дәріс жоспары

1.Маңдайлы кедергі туралы түсінік.

2. Қанаттәріздес ұзындық қиманы айналып өту

3. Н.Е. Жуковский теоремасы

4. Профильдер торы туралы теория

5. Шекаралық қабат туралы ұғым. Ұзын ақпалы (обтекаемый) пластинадағы ламинарлы және турбулентті шекаралық қабат.

Дәрістің қысқаша мазмұны

Егер қатты денені сұйқтық айналып өтсе немесе сол қатты дене қозғалмайтын сұйықтыққа толтырылған ортада қозғалса, онда дене мен сұйықтықтың арасында гидроаэродинмикалық әсерлесу пайда болады. Егер денемен сұйықтықтың салыстырмалы жылдамдықтары бірдей болса онда екеуінде де күштерді анықтайтын шамалар бірдей болады.

Қатты денені асиметриялы айналып ағатын болса онда, сұйықтықтың денеге әсер ететін күш бағыты қозбаған v_¥ ағын бағытымен сәйкес келмейді (денеден шексіз алыс жердегі жылдамдықтар). Бұл жағдайда күшті құраушыларға жіктеуге болады (7.1 сурет): көтергіш күш R_y=Rcosa, v_¥, векторын нормаль бағыттталады, және маңдайлы кедергі күші R_x=Rsina,v_¥.векторының бағытымен сәйкес келеді.

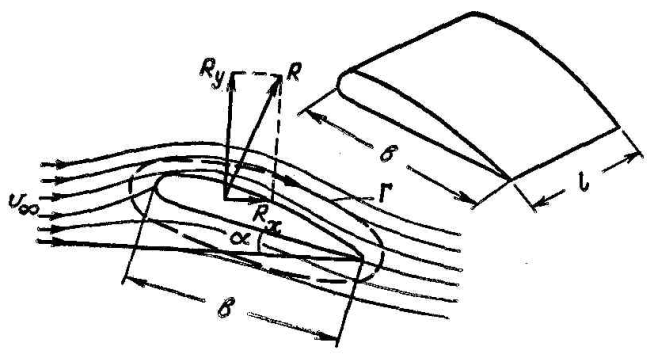
7.1сурет– Ағын айналып өтетін қанатқа әсер ететін күштер

R_y көтергіш күші жасаған және R_x,маңдайлы кедергі күшінен әлде қайда үлкен денені сұйық айналып өткенде пайда болатын денені, қанат деп атайды. Алғаш рет қанттың рационалды пішінін Н. Е. Жуковский ұсынған R_y/R_x =50÷70,

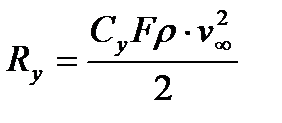, (7.1)

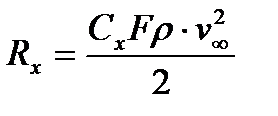, (7.2)

мұнда С_у, С_х – сәкесінше көтергіш күш және маңдайлы кедергі күштерінің коэффициенті; F = bl – қанат ауданы; b – қанаттың ені; l – ұзындығы (размах).

С_у и С_х коэффициенттері қантың a шабуыл бұрышына және оның бетінің тегістігіне байланыты профиліне тәуелді. Қанаттарды аэродинамикалық құбырларда үрлеудің арқасында қанаттың аэродинамикалық сипатын анықтайтын C_y=f(a) и C_x=f(a), тәуелділігі анықталған.

Көтергіш күшті ассиметриялық профильді айналып өту кезіндеде алуға болады, мысалы, цилиндр тәріздес айналмалы дене – ротор, немесе құйын (7.2 сурет). Сұйықтықтың тұтқырлылығы салдарынан ротор айналасында сұйықтықтың цилиндрлі қозғалысы пайда болады с_и, ол негізгі v_¥, жылдамдығына қосылады, сонвң салдарынан берілген айналу бағытында жылдамдық (v_¥ - с_и) ротордың астында азаяды, ал ротордың үстінде (v_¥ + с_и) - ұлғаяды. Егер қимадағы толық ағын бірдей болса, онда ротордың астындағы және үстіндегі жылдамдықтар айырымының арқасында, Бернули теңдеуіне сәйкес, Р₁ қысымы Р₂ –дан асып түседі, ақырында көтергіш күш пайда болады R_y=(P₁-P₂)F. Ол эффектті – Магнуса эффектідеп аталады.

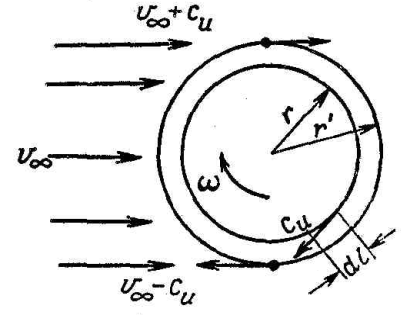
7.2 сурет – Айналмалы роторды ағынның айналып өтуі

Осылайша, роторды айналып өту кезінде тура қантта болатын процестер өтеді. Ротордың немесе қанттың айналасында пайда болатын кинематикалық өріс – жылдамдық циркуляциясы деп аталады.

Н. Е. Жуковский, қанаттың көтергіш күшінің көзі ол профилінің айналасындағы сұйықтықтың циркуляциялық қозғалысы екенін дәлелдеді. (7.1 сурет) және көтергіш күшпен R_у және жылдамдық Г циркуляцисының арасындағыбайланыс:

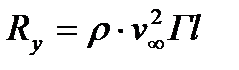. (7.3)

Көтергіш күштің бағыты v_¥ жылдамдық векторының циркуляциялық қозғалысқа қарай 90⁰ бұрылумен анықталады.

(7.1) және (7.3) теңдеулерінің бірінші бөліктері теңестіре отырып, Г профиль айналасындағы циркуляцияның мәнін анықтаймыз:

.

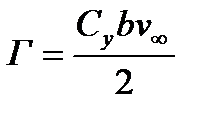Ол пайымдама, С_у тәжірибелік шамасы мен Г есептік шамасының байланыстырады. 1904 жылы орыс ғалымы Л. Прандтль ашқан қабырға жанындағы қозғалыстарының ерекшеліктерін ескеру үшін, шек аралық қабат теориясы қолданылады. Шекаралық қабатта ағын екі өлшемді және үш өлшемді болуы мүмкін. Екі өлшемді қозғалыстың жылдамдық векторлары бір жазықтықта жатады. Үш өлшемді қабаттардың жылдамдық векторлары кей жағдайларда комплонарлы болуы мүмкін.

Үдемелі ағынның қозғалыс режиміне байланысты шекаралық қабат түрлі структураға ие болады. Егер ағын ламинарлық болса, шекаралық қабатта ламинарлық болатыны өте ықтимал.

Ұсынылатын әдебиет

1. Б. Т. Емцев. Техническая гидромеханика М.: Машиностроение, 1987.

2. В.Г. Гейер и др. Гидравлика и гидропривод. М.: Недра, 1991.

3. Р. Р. Чугаев. Гидравлика. Ленинград: Энергия, 1975.

4. В.А. Кудинов, Э.М. Карташов. Гидравлика. М.: Высшая школа, 2007.

5. Э.П. Волчков, В.П. Лебедев. Тепломассообмен в пристенных течениях. Новосибирск, НГТУ, 2003.

СӨЖ-ге арнайы бақылау сұрақтары

1. Денеге сұйықтық жағынан әсер ететін көтергіш күштің анықтамасы.

2. Тілікте шекаралық қабатты есептеу

3. Н.Е. Жуковский теоремасы

8 тақырып. Ағынның екі фазасы (3/1/1/1 сағ)

Дәріс жоспары

1.Екі фазалық ағын және олардың сипаттамсы туралы ұғым

2. Қатты дененің бөлшектерінің транспорты

3. Шектік жылдамдық

4. Вертикальді трубкадағы бөлшектердің ушуы

5. Пневмо транспорт кезіндегі құбырлардың кедергісі.

6. Газ сұйықтықтардың қоспасының құрылымдары

Дәрістің қысқаша мазмүны

Алдындағы тараулардағы заңдылықтары біртекті орта үшін де әділетті.Көп процесстерде металлургия және теплоэнергетикада екі фазалық жүйелермен әрекеттесуге тура келеді. Мұндай жүйелерде біртекті немесе біртекті және дисперстік фазаларды айырады.

Екіфазалық жүйелер агрегаттық күйіне қарай жіктеледі. Біртекті де дисперсиялық фазалард үш агрегаттық күйлерде бола алады.

9 тақырып.Ағынды батыру (3/1/1/1 сағат)

Дәрістің жоспары

1.Ағындық шек – аралық қабат

2. Ағындардың классификациясы

3. Еркін турбулентті ағын

4. Жылдамдықтырдың таралу заңы

5. Бастапқы негізгі аймақ. Оралған ағын

Дәрістің қысқаша мазмұны

Сұйықтық ағыны, қатты қабырғалармен шектелмеген, тура солсияқты немесе басқа сұйықтық массасында қозғалып баражатқан еркін ағын деп аталады. Еркін ағындар батырылған және батырылмаған болуы мүмкін. Батырылған ағын сол сұйықтық кеңістігіне еніп жатқан ағынды атайды. 9.1 суретінде турбулентті батырылған ағынның құрылымы көрсетілген, d диаметрлі тетіктен ағып шыққан.

Турбулентті газ ағынының ерекшеліктері сол, оларда қоспалар концентрациясы, жылдамдық және температура сияқты параметрлердің беттің тангенциалды жаырауы бар. Ол бет тұрақсыз, соның арқасында онда узынынан және көлденеңінен тасымалданатын турбулентті құйындар пайда болады. Соңғылары, өзінің көлденең орын ауыстыру кезінде ағынның шетінен шығып кетедіда, өз импульстерін жанасып жатқан газдың қабатына береді, және сонымен қатар өзінің қозғалыс мөлшерінің бөлігін береді. Сонымен қатар ағынға қоршаған ортанының бөлшектері де кіріп үлгереді.

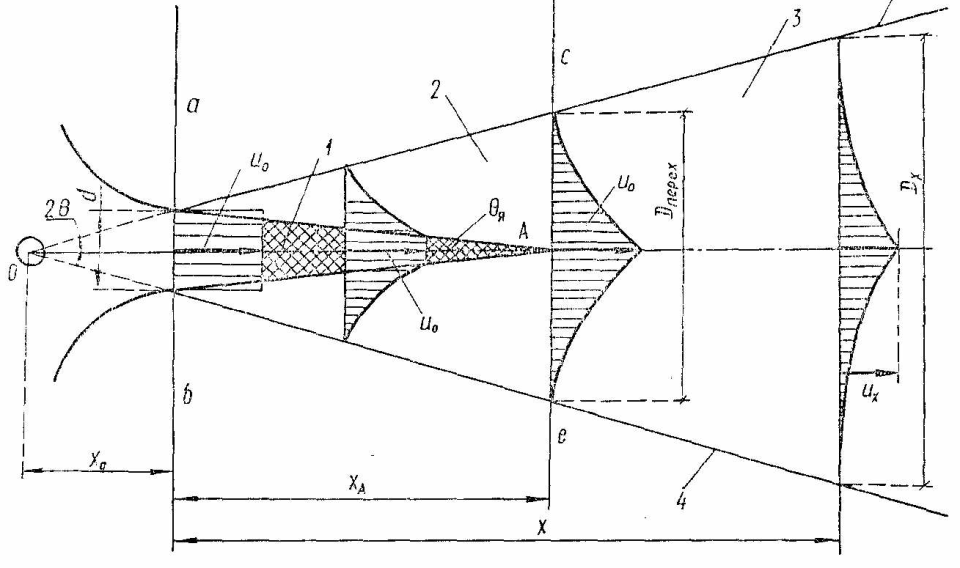
9.1 суреті – Турбулентті батырылған ағын құрылымы

0 – ағын полюсі; a-b –бастапқы қима; с-е – өтпелі қима; 1 – бірдей жылдамдықтар аймағы u₀; 2 – турбулентті зона; 3 – ағынның негізіг учаскесі; 4 – ағынның шекарасы.

Шекаралық ағындар қозғалысқа үлескен қоршаған газдың бөлшектерімен бірге еркін шекаралық турбулентті қабатты құрайды, оның қалыңдығы жылдамдық бағытында жуандайды. Егер соплоның шығыс қимасында жылдамдықтар біртекті таралса, онда басында ағын қимасын нольге тең. Ол жағдайда шек аралық қабаттың шектері ажыратылған беттер тәріздес болады. Тыныштық шектегі 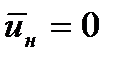бірлікті турбуленттік сорғыламаның таралуын қараймыз.

Сырт жағынан осындай сорғылаудың шекаралық қабаты тыныштық сұйықтығымен үйкеліседі, атап айтқанда, сырт жағынан деген беттің барлық нүктелерінде хось бойындағы жылдамдықтар нөл болғанды айтады. Сорғылаудың шекараларын осы берілген мәліметтерге сәйкес табу өте қиын, сондықтан шекаралық қабаттың қалындығын анықтағанда практикада сорғылаудың шекарасына 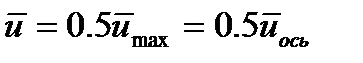барлық нүктелер бар бетті айтады.

Сорғылаудың шекаралық жағдайын оның ашылу бұрышы анықтайды, оның сәулелері болып ось пен сорғылау шекарасы болады. Сорғылаудың барлық учаскелерінде оның дамуы өзіндік ерекшеліктерге ие болғандықтан, ашылу шекарасы жалпы жағдайда сорғылаудың басынан қашықтық функциясы болады. Шүмектің қиылған жерінен қашықтығы сорғылау осьтің жылдамдығы қоршаған ортаны қорғау жылдамдығына тең болуды алысқа тиетін сорғылау деп атайды.

Эксперименттік мәліметтердің талдауы бойынша, турбуленттік сорғылаудың кинематикалық сипаттамаларының өзгеруі заңдылықтары онда үш учаскені белгілейді. Біріншісінде, бастапқы деп аталған және шүмектің 4-6 диаметрінде орналасқан, сорғылаудың ағыны ламинарлық және х > (4÷6)d_o болғанда ол турбулентті болады. Көп сараптамалар көрсеткендей, сорғылаудың негізгі қасиеті болып оның барлық ағындарындағы статикалық қысмының тұрақтылығы болады, соның салдарынан сорғылаудың жылдамдығы тұрақты болып қалады. Сондықтан шекаралық қабаттағы ішкі шекарада бастапқы учаскеде ағын жылдамдығы толу жылдамдығына тең ( ).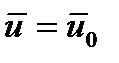

Бастапқы учаскеден кеткен сорғылаудың жайылуы оның қалындауында ғана емес, оның ось жағынан да жылдамыдықтың өзгеруінде де. Сорғылаудың бастапқы учаскесінің соңында еркін турбуленттік шекаралық қалындығы сорғылаудың ось жағына жетеді. Бастапқы учаскесінен кейін келесі ұзындығы ~(2 ÷ 4)d_o тең болғанда жылдамдық сорғылаудың ось жағынан азая бастайды. Ось жағынан жылдамдықтың өзгеруі негізгі учаскеде де (х > (8 ÷ 10) d_o болғанда) жалғасады.

Ұсынылатын әдебиеттер

1. Б. Т. Емцев. Техническая гидромеханика М.: Машиностроение, 1987.

2. В.Г. Гейер и др. Гидравлика и гидропривод. М.:Недра, 1991.

3. Р. Р. Чугаев. Гидравлика. Ленинград: Энергия, 1975.

4. В.А. Кудинов, Э.М. Карташов. Гидравлика. М.: Высшая школа, 2007.

СӨЖ арналған бақылау тапсырмалары

1.Турбулентті батқан сорғылаудың есептеулері.

2. Турбулентті батпаған сорғылаудың есептеулері.

3. Бұралған сорғылауды анықтау.

10 Тақырып.Газ динамикасы (3/1/1/1 сағ)

Дәріс жоспары

1.Үлкен жылдамдықтардағы газдың сығылуы

2. Газдардың бір өлшемді қозғалысының негізгі теңдеулері.

3. Мықтылар және әлсіздер

4. Газ ағынындағы әлсіз қозулардың таралуы

5. Тығыздалу ауытқуы

6. Ауытқу кезіндегі газ параметрлері

Дәрістің қысқаша мазмұны

Бернулли теңдеуідифференциалды түрде:

.

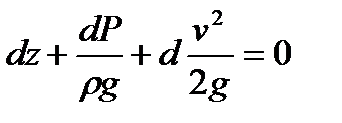Газдар үшін,

.

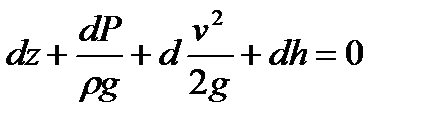Осы теңдеуді Δl элементар ағынының ұзындығы бойынша интегралдай отырып

.

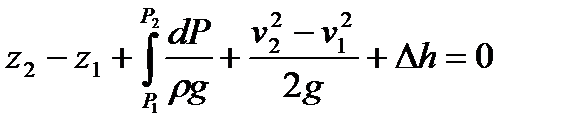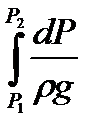шамасын, қысымның функциясы ρ тығыздығын табу арқылы, анықтауға болады. Осы функцияның сипаты термодинамикалық процесске тәуелді.

Политропа теңдеуінен 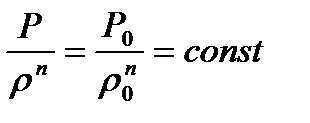ρ = f(P) функциясын табамыз, ол мына түрде болады 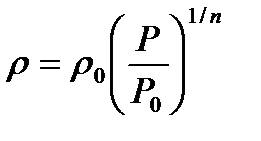. Қойғаннан кейін

,

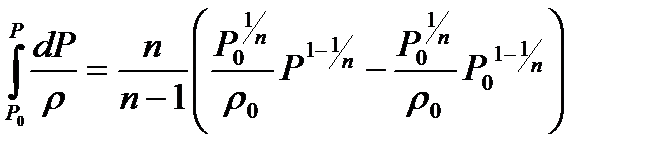Іздеп отырған интегралдың шешімі

.

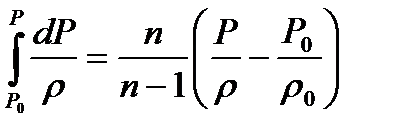Бернули теңдеуіне қоя отырып келесі теңдеуді аламыз

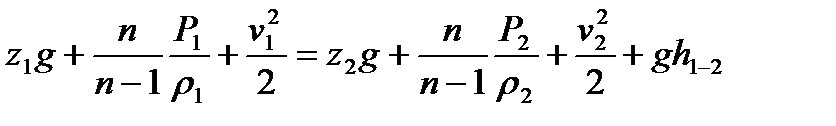. (10.1)

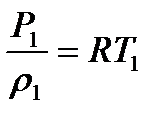, ал 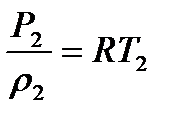біле отырып, осы теңдеуге мына түрді беруге болады

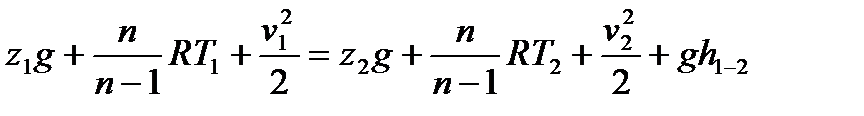, (10.2)

мұндаh_1-2 – жоғалтылған меншікті энергия;

R – меншікті газ тұрақтысы;

g – еркін түсу үдеуі.

Адиабаталық процесс кезінде газ қозғалысы дәл сол теңдеулермен сипатталады, бірақ политропа көрсеткіші n адиабата көрсеткішіне алмастырылады k. Сондықтан адиабаталық процесс кезінде Бернулли теңдеуі былай болады

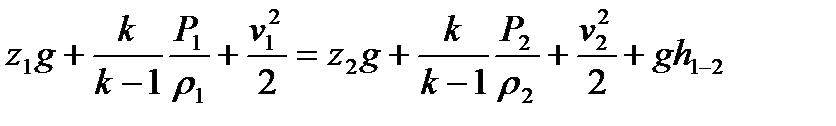(10.3)

Немесе

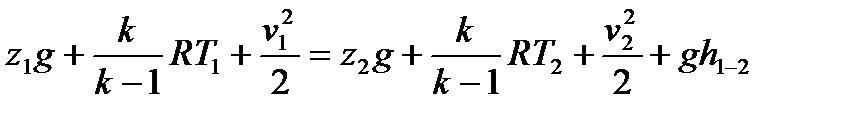. (10.4)

Изотермиялық процесс кезіндегі газ қозғалысын алайық, 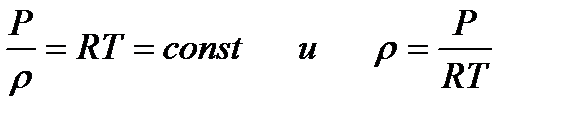шарттары сақталатын кезде. Бұл жағдайда, температура тұрақтысын ескере отырып, 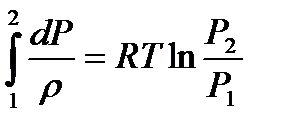, сонда изотермиялық процесс үшін Бернули теңдеуі

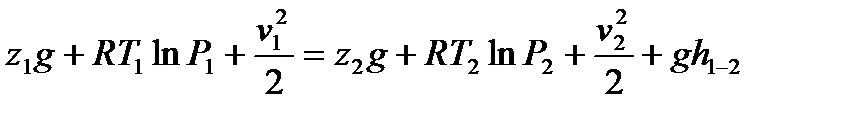. (10.5)

Газ құбыржолдарын есептегенде, z₁- z₂ = Δz шамасын ескермеуге болады,Δz = 0 екен деп; Бернули теңдеуі қысқаша былай жазылады:

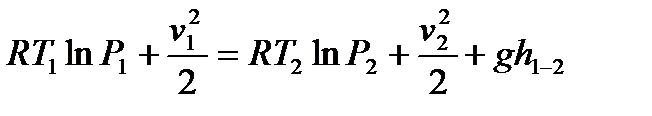. (10.6)

Осы теңдеудің қолданылуын қарастырайық.адиабаталық процесс кезінде Бернули теңдеу былай жазылады (gh_1-2 шамасын ескермейміз):

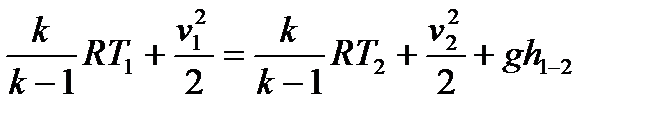,одан ,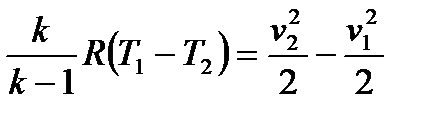

немесе

.

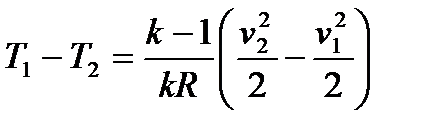Бірақ адиабаталық процесс үшін k = 1.4 деп есептеуге болады, R газ тұрақтысы 287,14 Дж/(кг×К) болады.

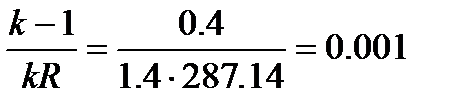, откуда .

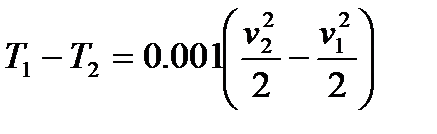Бұл теңдеу егер газ құбырынының бастапқы және соңғы қималарда жылдамдық квадратының жартысы ~ 1000 м болса, онда температуда1 градусқа өзгереді. Осылайша, практика жүзінде жылыту изоляциялары жоқ газ құбырларын изометрикалық процес кезендегі сияқты есептеуге болады.

Көп жағдайларда газдың жоғары жылдамдықпен қозғалуын кездестіреміз. Осындай ағындардың физикалық процесі өте қиын, және оның заңдылықтарын зерттеу газдық аэродинамика деп аталатын пәннің еншісінде.

Бұл жерде тек газдың құбырлармен жоғары жылдамдықпен ауыспалы қимадағы ерекшеліктерін қараймыз. Ол деген газдың жылдамдығы құбыржолдың қимасының өсуіне қарай әрқашан шегімейді, ол жоғарлауы да мүмкін (егер газ жылдамдығы дыбыс жылдамдығынан жоғары болса).

Белгілі болғандай, d ауыспалы диаметрі сығылмаған сұйықтықтың құбыр бойы қозғалысы, сонымен қатар, S көлденең қимасының ауыспалы ауданы да, орташа жылдамдық тұтас теңдеуге сәйкес d азаяды және керісінше d жоғарлағанда кемиді.

Газдың қозғалысы кезінде бұл қатынас сақталмауы да мүмкін, мысалы, жабысқақ емес газдық сұйықтықтың тұрақталған қозғалысында да. Құбыржолдардың массалық шығынның тұрақтылық жағдайы бойынша Q_ρ = ρvS = const. Бұл теңдеуді дифференциальдағанда, былай болады:

dQ_ρ = vSdρ + ρvdS +ρSdv = 0

және оны ρvS көбейтіндісіне бөліп, табамыз

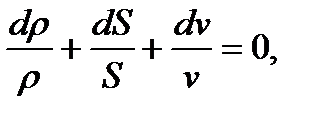
Одан болады

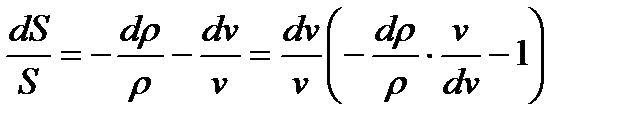. (10.7)

Бернулли теңдеуін пайдаланып dv неге тең екенін анықтаймыз. Егер мәселе үшін көлденең құбыр алсақ, онда z = const және dz = 0.Бұл жағдайда Бернулли теңдеуі жеңілденеді:

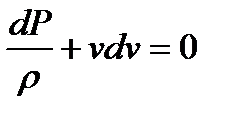, одан .

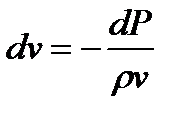(10.7) орнына қойып аламыз

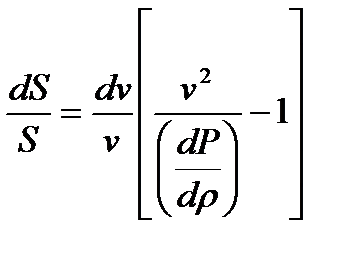. (10.8)

Белгілі болғандай, дыбыс жылдамдығы с (қатты деформация жылдамдығын тарату) мына формуламен 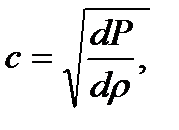анықталады, 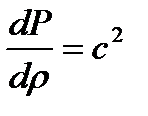ескереотырып. Сондықтан, (10.8) орнына жазамыз:

.

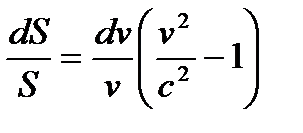Газдың қозғалыс жылдамдығының v дыбыс жылдамдығына қатынасынс Маха М саны деп атайды.

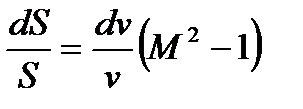. (10.9)

Осы теңдеуден екі қорытынды шығады.

1. Егер v < c,яғни егер газдың жылдамдығы дыбыс жылдамдығынан кем болса (мұндай жылдамдықты дыбысқа дейінгі жылдамдық деп атайды), онда М < 1 и (М² – 1) < 0 болады, яғни жақшадағы мағына теріс болады, ал сонда dS>0 dv < 0. Басқа сөзбен айтқанда, қиманың ауданы ұлғайса, газдың жылдамдығы азаяды (сығылмалы сұйықтыққа да).

2.Егер v > c и М > 1 болса және сондықтан(М² – 1) > 0, яғни дыбыс жылдамдығынан жоғары жылдамдықтар (аса дыбысты жылдамдық кезінде), dS > 0 болғанда dv > 0 . Сондықтан, қиманының ауданы ұлғайғанда газдың қозғалыс жылдамдығы жоғарлайды.

Ұсынылған әдебиеттер

1. Б. Т. Емцев. Техническая гидромеханика М.: Машиностроение, 1987.

2. В.Г. Гейер и др. Гидравлика и гидропривод. М.:Недра, 1991.

3. Р. Р. Чугаев. Гидравлика. Ленинград: Энергия, 1975.

4. В.А. Кудинов, Э.М. Карташов. Гидравлика. М.: Высшая школа, 2007.

СӨЖ арналған бақылау тапсырмалары

1. Кинематика және динамиканың негізгі теңдеулерімен газдың қозғалысы кезінде оның параметрлерін есептеу және анықтау.