Образование неметаллических включений
Образование любой новой фазы, например оксидов, в пересыщенном расплаве начинается с образования зародышей. Для определения критического диаметра зарождающейся фазы (зародыша) можно использовать уравнение Томпсона для давления насыщения мельчайших капель
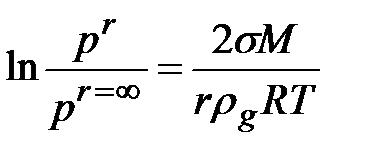или
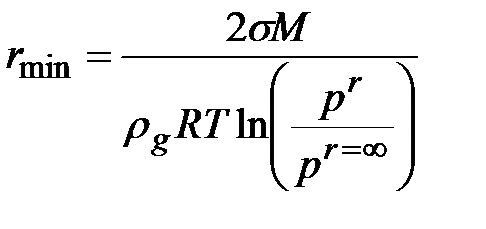, (1.31)
где М – молекулярная масса; pr – давление испарения капли радиусом r; pr=¥ – давление пересыщения.
Отношение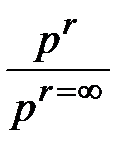 
в случае образования газовой фазы (например, СО) равно отношению парциального давления газа в пузыре к равновесному давлению в пузыре в случае плоской границы раздела фаз 
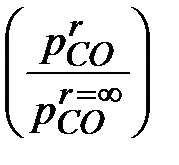, а в случае образования твердого зародыша – отношению концентраций оксида 
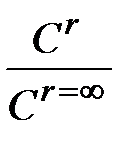(пересыщение).
Величину пересыщения при раскислении металла можно представить в виде
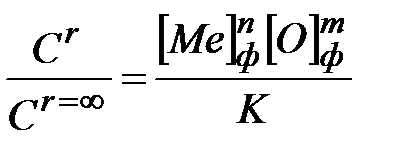, (1.32)
где K – константа равновесия реакции раскисления; [Me]ф, [O]ф – фактическая концентрация элемента – раскислителя и кислорода, растворенных в жидком металле; n, m – стехиометрические коэффициенты реакции окисления.
Согласно уравнению (31), чем выше пересыщение расплава, тем меньше критический радиус зародыша и выше вероятность его появления. Образование зародышей может происходить в объеме (гомогенное образование зародышей) и на границе раздела фаз металл – шлак, металл – огнеупорная футеровка, металл – газовый пузырь и т.п. Интенсивность гомогенного образования новой фазы определяется соотношением
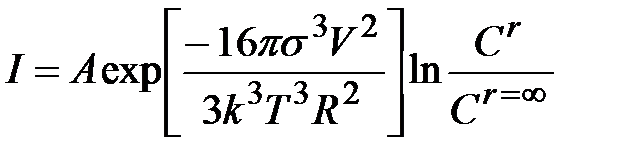, (1.33)
где А – коэффициент, близкий по порядку к числу Авогадро; V – молекулярный объем зародыша; k – постоянная Больцмана.
Рассмотрим механизм роста зародыша, предполагая его сферичность и сферическую симметрию концентрационных полей вокруг зародыша. Поступающий за счет диффузии продукт раскисления осаждается на поверхности зародыша. Поступающий за счет диффузии продукт раскисления осаждается на поверхности зародыша соответственно своему молекулярному объему и увеличивает объем частицы со скоростью
,
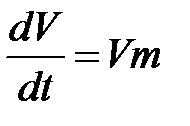где m – диффузионный поток массы на поверхность частиц.
Учитывая, что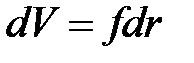 
, где f – площадь поверхности зародыша представим последнее выражение в виде
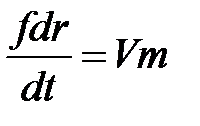. (1.34)
Диффузионный поток на поверхность частиц в сферических координатах (с учетом сферической симметрии)
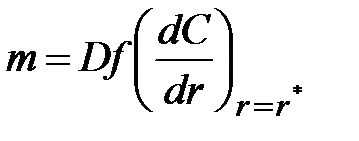, (1.35)
где r* - радиус частицы.
В условиях стационарности процесса массопереноса, изменение концентрации по радиусу имеет линейный характер, т.е.
,
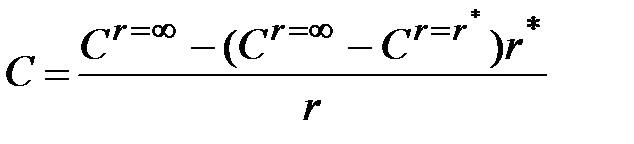где 
и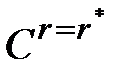 
- соответствующие концентрации продукта раскисления в объеме металла и на поверхности зародыша.
Дифференцируя последнее выражение, получим
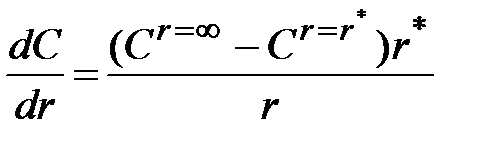, или при r= r*
.
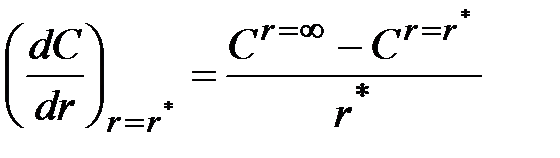После подстановки полученного выражения в формулу (35)
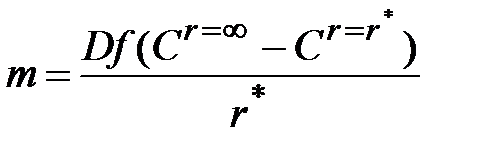. (1.36)
Подставляя (36) в формулу (34), определим скорость роста зародыша
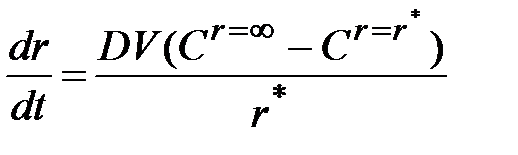. (1.37)
Закон изменения во времени радиуса частицы получим, разделив переменные в (37)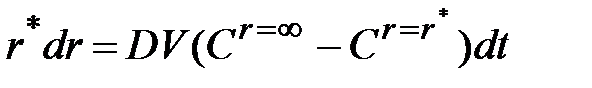 
, и, интегрируя,
.
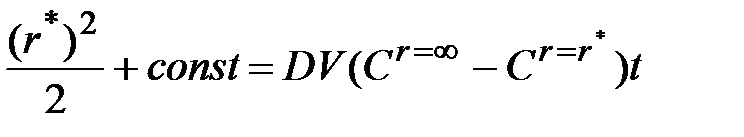Константу интегрирования определим из граничных условий: при t=0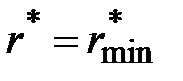 
. Тогда 
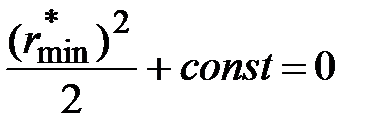и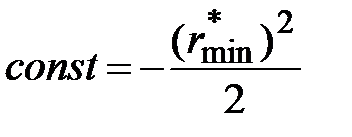 
.
Т.о., уравнение, описывающее рост зародышей во времени, имеет вид
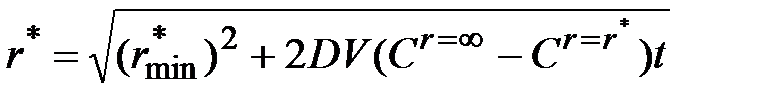. (1.38)
Рассматривая по аналогии с газовым (15) или паровым (27) пузырем равновесие сил, действующих на образовавшийся пузырь СО, несложно найти отрывной радиус пузыря СО. Он зависит от величины краевого угла смачивания, без учета сил гидродинамического сопротивления.
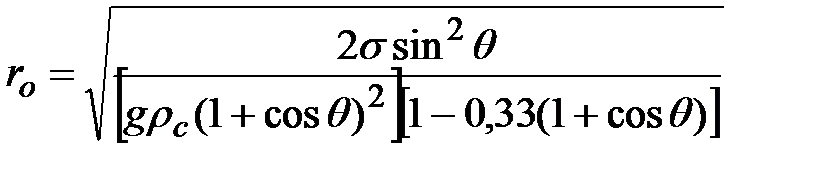; (1.39)
при q<90о
,
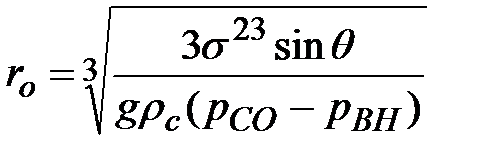где рВН – вешнее давление на образующийся пузырь СО, учитывающее атмосферное давление рат и гидростатическое давление металла рМе и шлама ршл.
РВН=рат+рМе+ршл.
Дата добавления: 2015-12-26; просмотров: 864;