Образование пузырей при кипении жидкости
Газовые пузыри могут возникнуть на непроницаемой поверхности вследствие диффузии растворенного в жидкости газа или в результате испарения жидкости. В большинстве случаев образование зародышей газовой фазы происходит на микровпадинах поверхности, причем минимальный радиус образовавшегося зародыша определяется в случае кипения перегревом слоя жидкости вблизи стенки 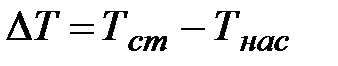 относительно температуры насыщения при данном давлении над плоскостью.
относительно температуры насыщения при данном давлении над плоскостью.
Образование пузыря ведет к искривлению поверхности раздела фаз, вызывающему скачок давления, обусловленный поверхностным натяжением и определяемый по формуле Лапласа:
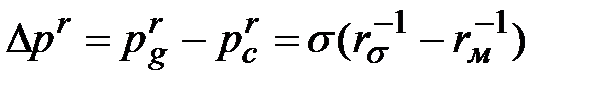 , (1.17)
, (1.17)
где 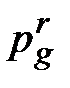 ,
, 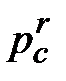 – давление на границе раздела фаз со стороны пара и жидкости;
– давление на границе раздела фаз со стороны пара и жидкости; 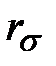 и
и 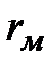 – большой и малый радиусы пузыря эллипсовидной формы.
– большой и малый радиусы пузыря эллипсовидной формы.
В случае сферической формы образовавшегося пузыря 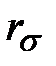 =
= 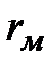 =
= 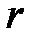
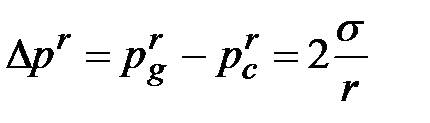 . (1.18)
. (1.18)
Если 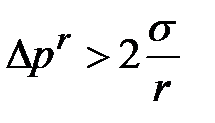 , то образовавшийся пузырь будет расти; если
, то образовавшийся пузырь будет расти; если 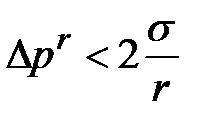 – пузырь сконденсируется.
– пузырь сконденсируется.
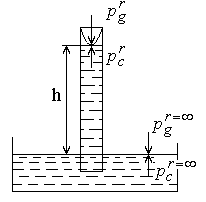 Рис. 2
Рис. 2
| Равновесное давление 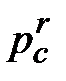 жидкости, окружающей газовый пузырь радиусом r, будет отличаться от равновесного давления жидкости жидкости, окружающей газовый пузырь радиусом r, будет отличаться от равновесного давления жидкости 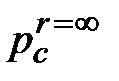 на плоской поверхности раздела фаз (рис. 2) на величину на плоской поверхности раздела фаз (рис. 2) на величину
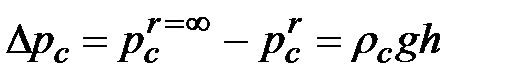 . (1.19) . (1.19)
|
Аналогично для газовой фазы
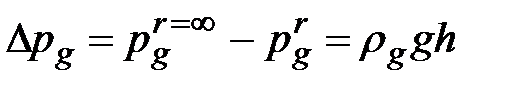 . (1.20)
. (1.20)
Вычитая уравнение (20) из уравнения (19), получим
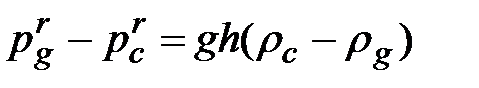
или, принимая во внимание соотношение (18)
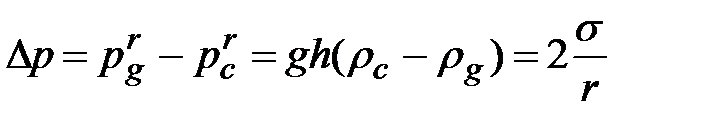 .
.
Отсюда
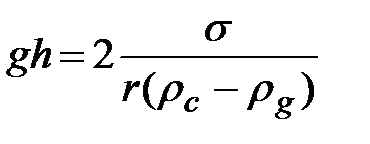 и
и
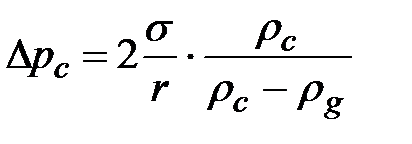 . (1.21)
. (1.21)
Соответственно, этому превышению давления жидкости при наличии равновесия с насыщенным паром в пузыре для переноса пара из жидкости необходим перегрев последней на
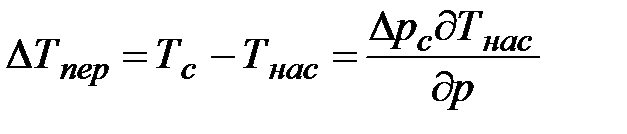 . (1.22)
. (1.22)
По формуле Клаузиса–Клайперона
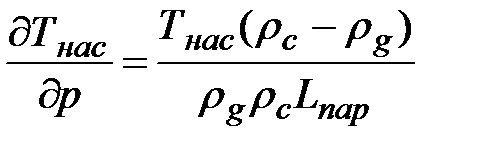 , (1.23)
, (1.23)
где Lпар – скрытая теплота парообразования.
Подставляя формулы (21) и (23) в уравнение (22), получим
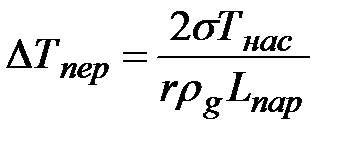 . (1.24)
. (1.24)
Их формулы (24) можно получить значение минимального зародыша первого пузыря, соответствующего данному перегреву жидкости у поверхности нагрева, т.е.
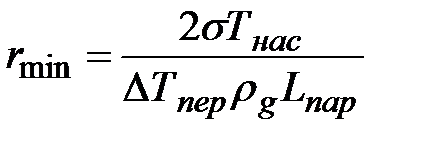 . (1.25)
. (1.25)
Образовавшийся зародыш радиусом rmin начинает расти, причем скорость роста сферического пузыря в жидкости, полностью прогретой до температуры насыщения, определяется величиной теплового потока, подводимого к поверхности пузырька и затрачиваемого на испарение жидкости. Вследствие малых размеров пузырька перенос тепла в жидкости осуществляется преимущественно за счет молекулярной теплопроводности и в этом случае число Нуссельта отвечает минимальному значению
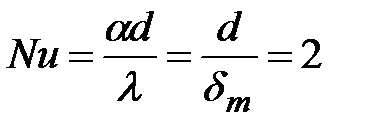 , т.е.
, т.е. 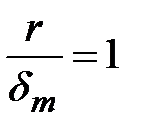 ,
,
где dт – толщина теплового пограничного слоя.
Пренебрегая изменением давления в пузыре, можно записать
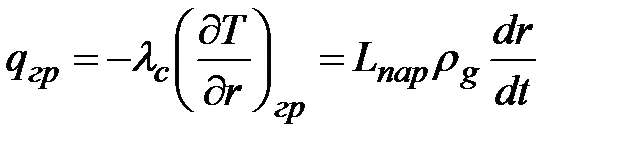 ,
,
Или, учитывая предыдущее соотношение,
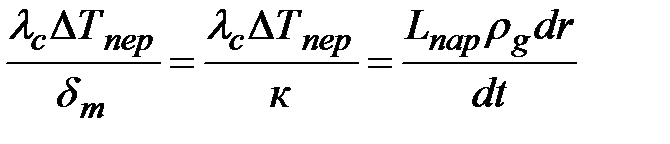 .
.
Отсюда легко получить уравнение роста пузыря:
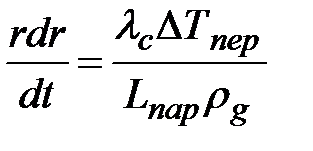 .
.
Интегрируя данное выражение в пределах от rmin до r , получим
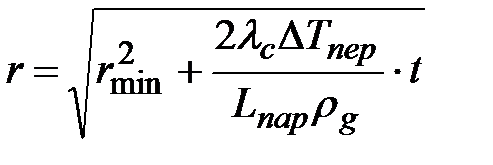 . (1.26)
. (1.26)
Отрывной радиус пузыря определяется также, как и в случае продувки жидкости (15), взаимодействием подъемной силы, отрывающей пузырь от поверхности, силы гидравлического сопротивления жидкости и силы поверхностного натяжения, прижимающих ножку пузыря к стенке, т.е.
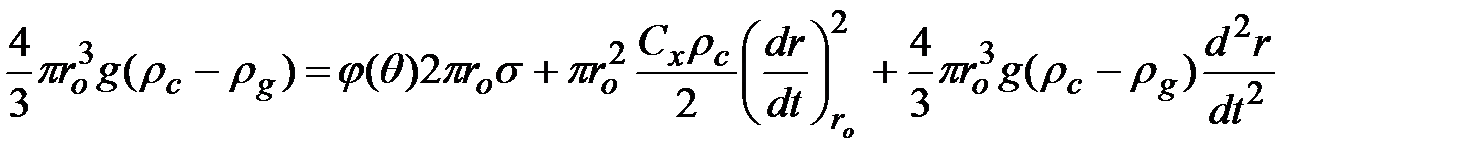 , (1.27)
, (1.27)
где последний член правой части уравнения характеризует инерционную силу, а j(q) – некоторая функция краевого угла смачивания q, учитывающая изменение q в реальных условиях роста пузыря.
На основании этого уравнения была получена обобщенная зависимость для расчета отрывного диаметра пузыря 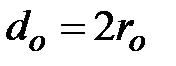 .
.
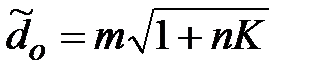 , (1.28)
, (1.28)
где 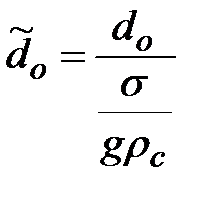 ;
; 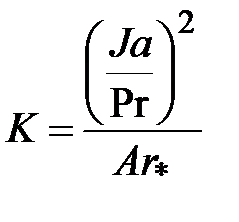 ;
; 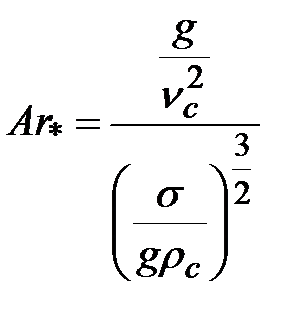 – модернизированный критерий Архимеда;
– модернизированный критерий Архимеда; 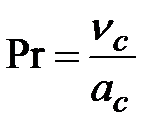 – критерий Прандтля;
– критерий Прандтля; 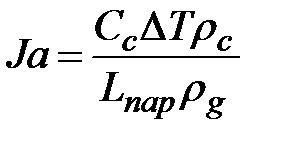 – критерий Якоба, характеризующий отношение количества теплоты, затраченной на нагрев единицы объема жидкости, к объемной теплоте парообразования; m=0,25; n=105 – эмпирические коэффициенты.
– критерий Якоба, характеризующий отношение количества теплоты, затраченной на нагрев единицы объема жидкости, к объемной теплоте парообразования; m=0,25; n=105 – эмпирические коэффициенты.
Из соотношения (28) следует, что отрывной диаметр пузыря обратно пропорционален плотности пара. В случае кипения при пониженном давлении отрывной диаметр пузыря резко увеличивается, частота их образования уменьшается. При достаточно высоком вакууме отдельные пузыри вообще не образуются, а испаряющаяся жидкость образует паровую пленку на поверхности нагрева. Пренебрегая инерционной силой и силой гидравлического сопротивления в уравнении (27) получим
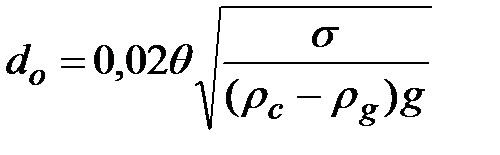 , (1.29)
, (1.29)
где q определяется в градусах (для воды q=50о).
Сопоставляя формулы (29) и (25), установили, что величина rо на несколько порядков больше rmin. Важное значение для процесса кипения имеет частота отрыва паровых пузырей от поверхности нагрева
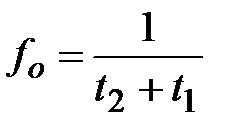 ,
,
где t1 – время роста пузыря до момента его отрыва от поверхности; t2 – время от момента отрыва до зарождения нового пузыря.
Для оценки частоты отрыва пузырей можно воспользоваться соотношением
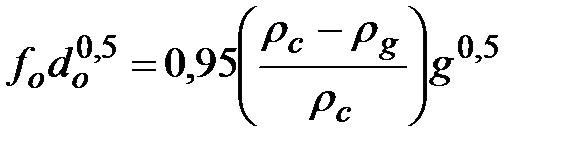 (1.30)
(1.30)
из которого следует, что на частоту отрыва сильно влияет давление и ускорение поля тяготения.
Дата добавления: 2015-12-26; просмотров: 2164;
