Основные законы переноса тепла и массы
Уравнения молекулярного переноса в сплошной среде:
тепла (постулат Фика)
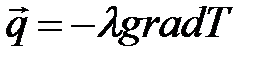 (2.1)
(2.1)
массы (общий закон Фика)
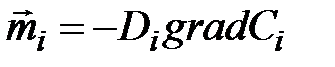 (2.2)
(2.2)
Уравнение конвективного переноса (в сферических координатах) в общем случае имеет вид:
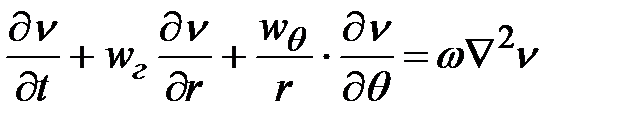 , (2.3)
, (2.3)
где n – температура (Т) для уравнений теплообмена и концентрация (С) для уравнений массообмена; w – соответствующий коэффициент температуропроводности (а) или диффузия (D); wr, wq - радиальная и тангенциальная составляющие скорости жидкости; Ñ2 – оператор Лапласа
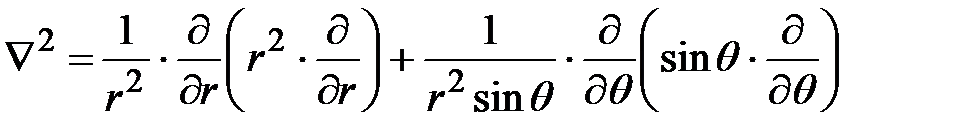 .
.
На границе раздела фаз процесс переноса описывается следующими соотношениями:
теплообмен между твердым телом и обтекающим его потоком жидкости или газа (закон Ньютона – Рихтмана):
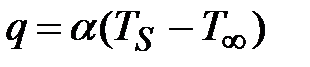 , (2.4)
, (2.4)
массообмен
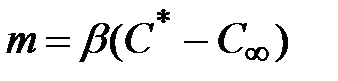 , (2.5)
, (2.5)
где b – коэффициент массоотдачи, м/с; С* – равновесная концентрация; С¥ – концентрация в невозмущенном потоке.
В случае дисперсной системы жидкость – жидкость или газ – жидкость:
Для теплообмена
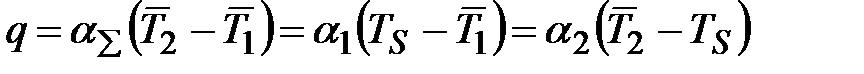 , (2.6)
, (2.6)
где 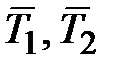 – средние по объему температуры соответствующих фаз; TS – температура на границе раздела фаз; a1, a2 – частные коэффициенты теплоотдачи; aS – суммарные коэффициент теплоотдачи:
– средние по объему температуры соответствующих фаз; TS – температура на границе раздела фаз; a1, a2 – частные коэффициенты теплоотдачи; aS – суммарные коэффициент теплоотдачи:
для массообмена
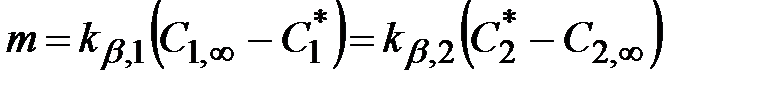 (2.7)
(2.7)
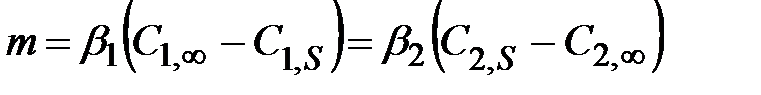 . (2.8)
. (2.8)
Согласно закону Генри
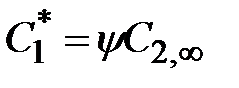 , (2.9)
, (2.9)
где y – коэффициент распределения, представляющий собой отношение к концентрации вещества в сплошной фазе (С2,¥), находящейся с ней в равновесии концентрации вещества в дисперсной фазе.
Связь между коэффициентами массопередачи и массоотдачи можно установить, полагая, что y, b1 и b2 не зависит от концентрации компонента, а на границе раздела фаз имеет место равновесие:
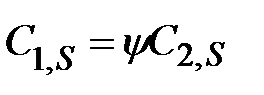 . (2.10)
. (2.10)
Из уравнений (2.7) – (2.8) получили
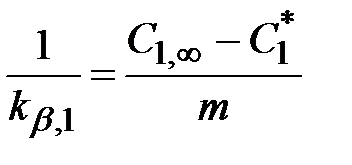 ;
; 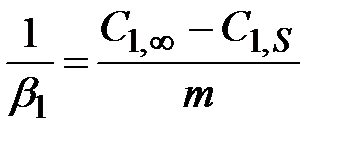 ;
; 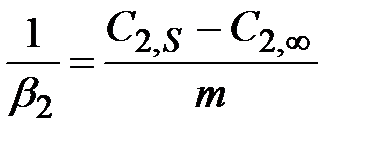 .
.
Умножая правую и левую часть последнего равенства на y и учитывая соотношение (2.9) и (2.10), запишем
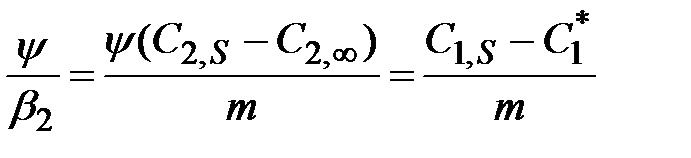 .
.
Поскольку 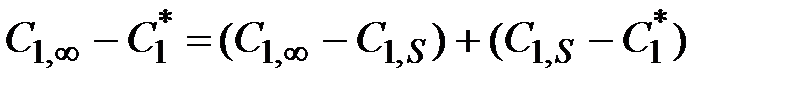 , то
, то
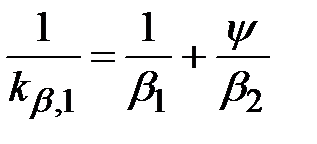 . (2.11)
. (2.11)
Аналогично можно получить
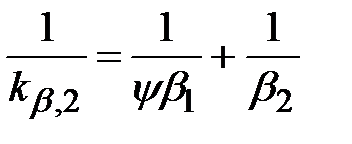 . (2.12)
. (2.12)
Соотношения (2.11) и (2.12) называют формулами аддитивности фазовых соотношений.
Дата добавления: 2015-12-26; просмотров: 1324;
