Внешняя задача тепломассообмена
При рассмотрении внешней задачи предположим, что внутри частицы градиента температуры и концентрации пренебрежимо малы по сравнению с соответствующими градиентами во внешнем потоке. В этом случае поток тепла или вещества можно найти с помощью уравнений баланса тепла и массы для внешнего течения. Поскольку тепловые и диффузионные процессы аналогичны, в дальнейшем использовали термины массопередачи. Рассматриваемый случай соответствует практике металлургического производства, поскольку растворимость многих газов (N2, H2, O2) в жидких металлах обычно невелика. В этом случае коэффициент распределения имеет большие значения и согласно уравнению
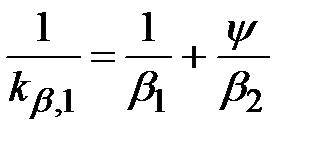
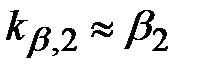 или
или 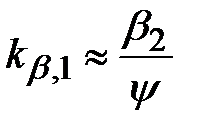 .
.
Растворимость газов в молекулах описывается законом Сиверста
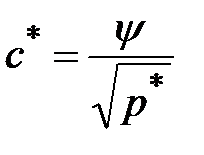 , (3.1)
, (3.1)
где с* – равновесная концентрация поглощаемого газа в жидкости, молярная доля; р* – равновесное парциальное давление поглощаемого газа над раствором; y – коэффициент распределения.
При малой растворимости газа вследствие медленного отвода газа от поверхности раздела фаз в глубь ванны концентрация газа на поверхности соответствует равновесной с газовой фазой 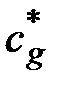 при парциальном давлении РS, мало отличающемся от равновесного значения.
при парциальном давлении РS, мало отличающемся от равновесного значения.
Примем, что частицу обтекает осесимметричный поток с заданным полем скоростей. Представим уравнение конвективного переноса в виде
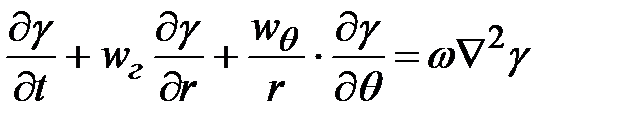
В безразмерном виде уравнение конвективного переноса имеет вид:
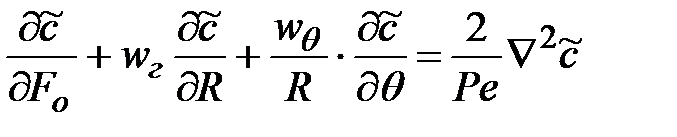 . (3.2)
. (3.2)
Краевые условия для внешней задачи массообмена имеют вид:
начальные
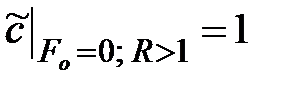 (3.3)
(3.3)
граничные (постоянство концентраций примеси на поверхности частицы и в потоке)
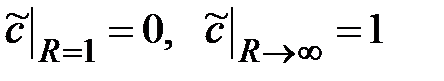 (3.4)
(3.4)
В уравнении (3.2) левая часть характеризует конвективный перенос вещества, правая – молекулярную диффузию. Соотношение между конвективным и диффузионным переносом вещества, характеризует критерий Пекле. При малых значениях критерия Пекле перенос вещества конвекцией пренебрежимо мал, по сравнению с молекулярной диффузией, что имеет метол при малой скорости движения потока и (или) малом размере частицы. При больших значениях критерия Пекле определяющим является конвективный перенос.
Критерий Пекле 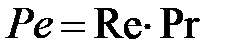 в задачах теплообмена, или
в задачах теплообмена, или 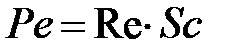 в задачах массообмена.
в задачах массообмена.
Массообмен при умеренных значениях критерия Пекле (1£Ре£103)
При умеренных значениях критерия Пекле система уравнений (3.2-3.4) решается численным методом, а результаты решения затем аппроксимируются расчетной формулой.
Для газового пузырька ( 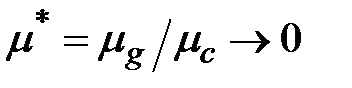 ), движущегося при Re<1, численные решения этих уравнений для значений Ре<103 с точностью 2-3% аппроксимируются формулой
), движущегося при Re<1, численные решения этих уравнений для значений Ре<103 с точностью 2-3% аппроксимируются формулой
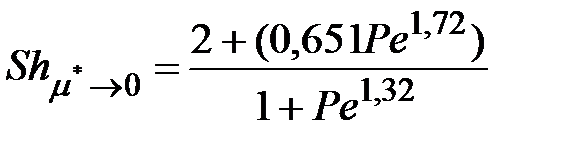 , (3.5)
, (3.5)
где Sh – число Шервуда, 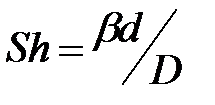 ; d – диаметр частицы, d=2ro.
; d – диаметр частицы, d=2ro.
Для твердой сферической частицы (m*®¥)
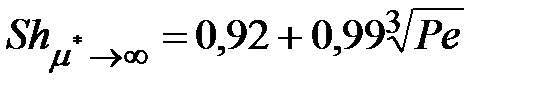 . (3.6)
. (3.6)
Для капли справедлива формула
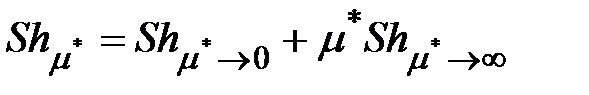 , (3.7)
, (3.7)
где 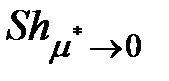 и
и 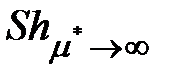 определяется по формулам (3.5) и (3.6) при фиксированных значениях Ре.
определяется по формулам (3.5) и (3.6) при фиксированных значениях Ре.
Увеличение коэффициента массоотдачи (критерия Шервуда) с ростом критерия Пекле определяется процессом формирования диффузионного пограничного слоя в лобовой части сферической частицы Увеличение критерия Ре ведет к уменьшению толщины образующегося диффузионного пограничного слоя, что в свою очередь, согласно формуле
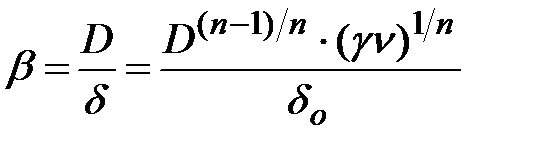
приводит к увеличению коэффициента массоотдачи b.
Массоперенос при больших значениях критерия Пекле (Ре>103)
При больших значениях критерия Пекле с достаточной для рпак4тических расчетов точностью процесс переноса можно считать установившимся и рассматривать его в приближении диффузионного пограничного слоя, уравнение (3.2) принимает вид
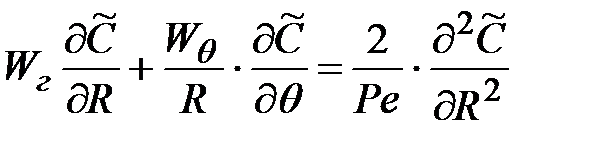 . (3.8)
. (3.8)
Уравнение (3.8) совместно с граничными условиями (3.4) можно решить аналитически, для чего его следует привести к уравнению Лапласа, воспользовавшись уравнением Прантдля–Мизеса. Последнее предполагает переход от переменных R, q к y, q, где 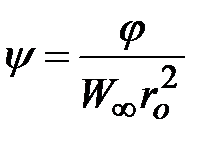 – безразмерная функция тока. Учитывая, что в пограничном слое сферической частицы
– безразмерная функция тока. Учитывая, что в пограничном слое сферической частицы 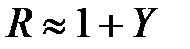 (
( 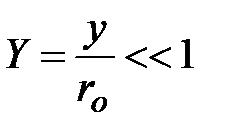 ), разложим безразмерную функцию тока вблизи поверхности частицы в ряд Тейлора
), разложим безразмерную функцию тока вблизи поверхности частицы в ряд Тейлора
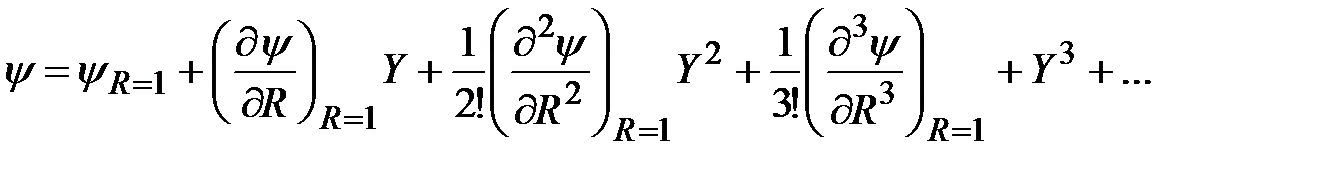 (3.9)
(3.9)
и сохранили лишь первый неисчезающий член.
Из уравнения (3.9) получили выражение для переменной Прандтля– Мизеса
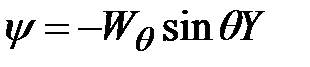 . (3.10)
. (3.10)
Переменная Прандтля–Мизеса для твердой среды
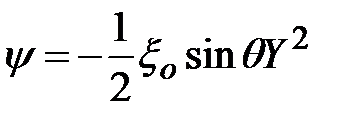 . (3.11)
. (3.11)
Введение новых переменных позволяет значительно упростить уравнение (3.8) и свести его у уравнению Лапласа
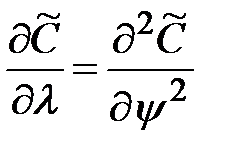 , (3.12)
, (3.12)
где 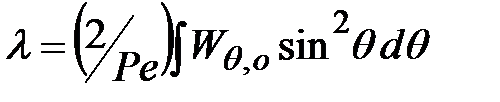 .
.
В новых переменных граничные условия имеют вид:
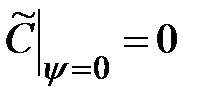 ; (3.13)
; (3.13)
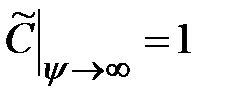 . (3.14)
. (3.14)
Полагая, что в точке набегания потока на сферу (точка q=0) концентрация вещества такая же, как на бесконечности, запишем
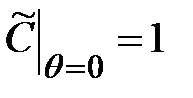 . (3.15)
. (3.15)
Решение уравнения (3.12) с граничными условиями (3.13) – (3.15) имеет вид
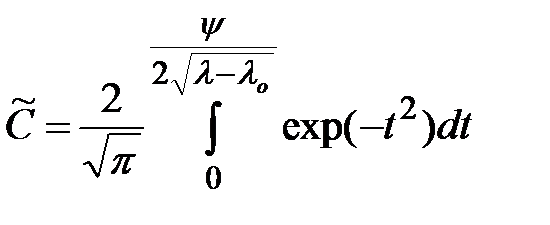 , (3.16)
, (3.16)
где lо – значение l при q=0.
Зная величину потока вещества, можно определить коэффициент массопередачи
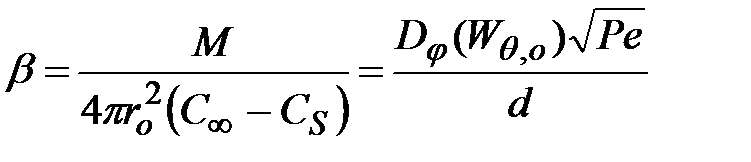
и величину числа Шервуда
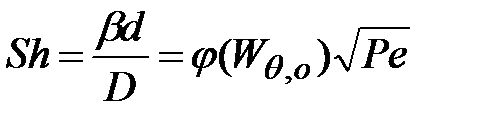 . (3.17)
. (3.17)
Дата добавления: 2015-12-26; просмотров: 1191;
