Теплообмен в неподвижном плотном слое. (Задача Шумана)

Рассмотрим процесс нагрева неподвижного слоя, состоящего из термически тонких частиц, одномерным потоком газа, движущимся вдоль оси у, принимая следующие допущения: слой состоит из частиц одинакового размера; теплообмен между потоком и слоем определяется законом Ньютона; коэффициент a_F одинаков по высоте и сечению слоя; теплофизические свойства частиц и газа не зависят от температуры; передача тепла в газе и в слое теплопроводностью отсутствует; поток газа равномерно распределен по сечению слоя. При принятых допущениях уравнения теплового баланса для элемента слоя объемом 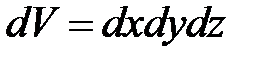и протекающего через этот элемент газа будут иметь вид:

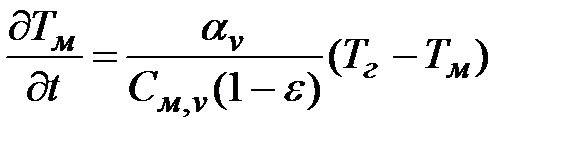; (3.22)

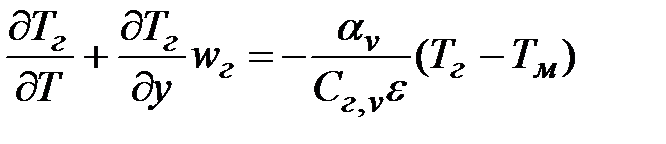, (3.23)

где Т_м, Т_г – температура слоя и протекающего через него газа; w_г – скорость газа в стесненном сечении, м/с; С_м,v, С_м,г – удельные объемные теплоемкости материала слоя и газа, дж/(м³ К).

Вводя обозначения

; ; ;

; ,

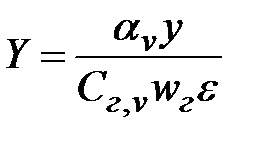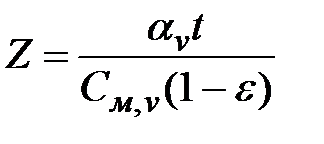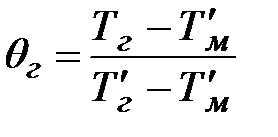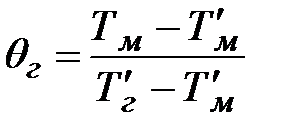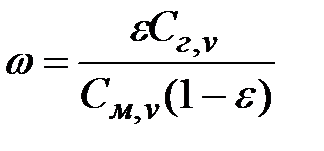где - температура (газа или материала) в начальный момент времени t=0.

Представим исходную систему уравнений в виде

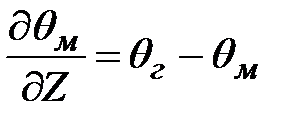; (3.24)

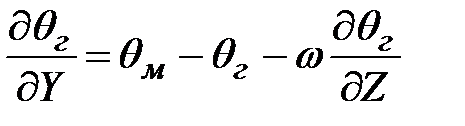. (3.25)

Краевые условия для рассматриваемой постановки задачи имеют вид

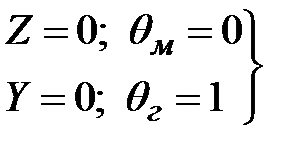(3.26)

Решение систем уравнений (3.24)-(3.26) получено Шуманом и в наиболее удобной форме может быть представлено следующим соотношением:

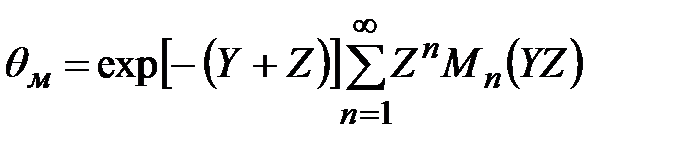(3.27)

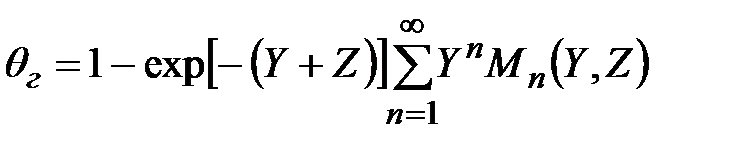(3.28)

где 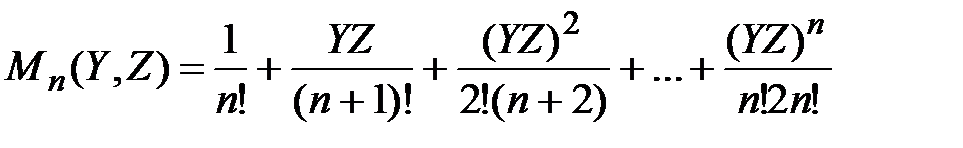- функция Бесселя первого рода нулевого порядка от мнимого аргумента.

Решение Шумана можно использовать и для расчета нагрева (охлаждения) слоя, состоящего из кусков, обладающим термическим сопротивлением.

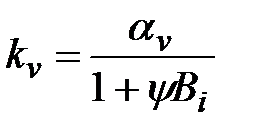. (3.29)

Анализ уравнений (3.27), (3.28) показывает, что температуры слоя и газа меняются по высоте слоя и во времени и зависят от размера частиц, порозности слоя, теплофизических параметров и скорости движения газа.