Дифференциальные уравнения конвективного теплообмена. Основные понятия конвективного теплообмена

Основные понятия конвективного теплообмена

Понятие конвективного теплообмена охватывает процесс теплообмена при движении жидкости или газа. При этом перенос теплоты осуществляется одновременно конвекцией и теплопроводностью.

Если в единицу времени через единицу контрольной поверхности нормально к ней проходит масса жидкости 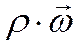, кг/(м²·с), где 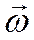– скорость, 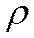– плотность жидкости, то вместе с ней переносится теплота, Вт/м²:

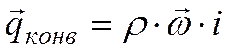
Конвекция теплоты всегда сопровождается теплопроводностью, т.к. при движении жидкости или газа происходит сопри­косновение отдельных частиц, имеющих различные температуры. В результате конвективный теплообмен описывают уравнением

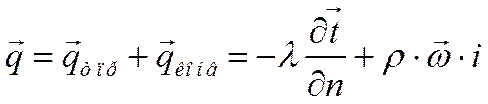
При расчетах конвективного теплообмена между текущей жидкостью и твёрдой стенкой используют закон Ньютона – Рихмана

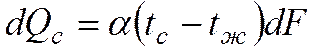
Коэффициент теплоотдачи α зависит от большого количества факто­ров. В общем случае α является функцией

- формы и размеров тела,

- ре­жима движения,

- скорости и температуры жидкости,

- физических па­раметров жидкости,

- других величин.

Чтобы привести жидкость в движение, к ней необходимо при­ложить силу. Силы, действующие на какой-либо элемент жидкости, можно разделить на массовые (или объемные) и поверхностные.

Массовыми называют силы, приложенные ко всем частицам жид­кости и обусловленные внешними силовыми полями (например, грави­тационным или электрическим).

Поверхностные силы возникают вслед­ствие действия окружающей жидкости или твердых тел; они приложены к поверхности контрольного объема жидкости. Такими силами являют­ся силы внешнего давления и силы трения.

Различают свободную и вынужденную конвекцию.

В пер­вом случае жидкость с неодно­родным распределением температуры, и, как следствие, с неоднород­ным распределением плотности, находится в поле земного тяготения. Поэтому в ней может возникнуть свободное гравитационное движение.

Вынужденное движение объема жидкости про­исходит под действием внешних поверхностных сил, приложенных на его границах, за счет предварительно сообщенной кинетической энер­гии (например, за счет работы насоса, вентилятора, ветра).

Вынужденное движение в общем случае может сопровождаться свободным движением. Относительное влияние последнего тем больше, чем больше разница температур отдельных частиц среды и чем меньше скорость вынужденного движения.

Дифференциальные уравнения конвективного теплообмена

Из уравнения 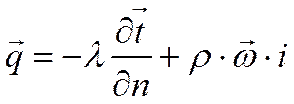следует, что плотность теплового потока в любой точке жидкости для каждого момента времени однозначно определяется, если известны поля температур, удельной энтальпии и скорости.

Связь между температурой и энтальпией может быть установлена следующим образом. Для реальной жидкости 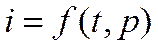, и согласно понятию о полном дифференциале

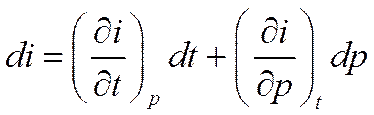
Отсюда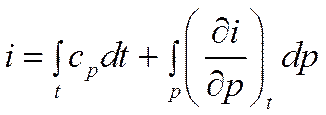

Для многих задач в предположении о несжимаемости жидкости (ρ=const) с достаточной степенью точности можно принять 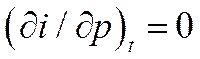, т.е. пользоваться соотношением, справедливым для термодинамически идеального газа 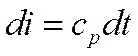и .

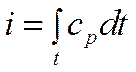Уравнение энергии.

Выведем диф­ференциальное уравнение, описывающее тем­пературное поле в движущейся жидкости.

При выводе будем полагать, что

- жидкость изотропна,

- её физические параметры постоянны,

- энергия деформации мала по срав­нению с изменением внутренней энергии.

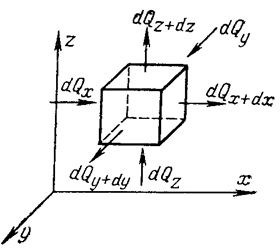Выделим в потоке жидкости неподвиж­ный относительно координатной системы эле­ментарный параллелепипед с реб­рами dx, dy и dz.

Через грани параллелепипе­да теплота переносится теплопроводностью и конвекцией; в общем случае в рассматривае­мом объеме может выделяться теплота внутренними источниками.

Вывод уравнения энергии, соответствующего принятым здесь усло­виям, был получен ранее:

,

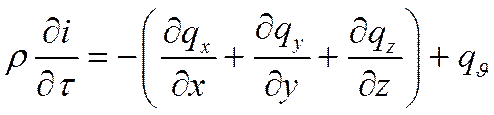Проекции плотности теплового потока 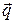на координатные оси Ох, Оу и Оz равны

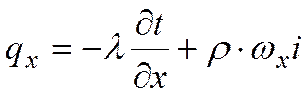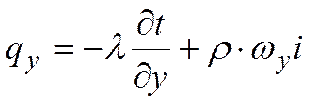, и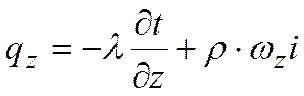

Подставляя значения q_x,q_y и q_z в уравнение Фурье, можно получить

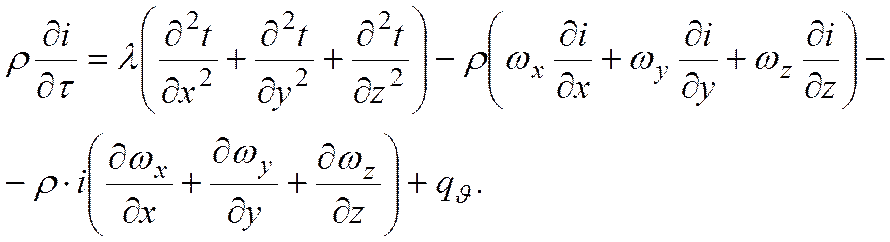
Для несжимаемых жидкостей (ρ=const) из закона сохранения массы следует:

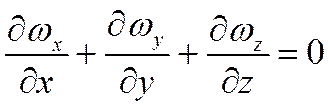
Тогда,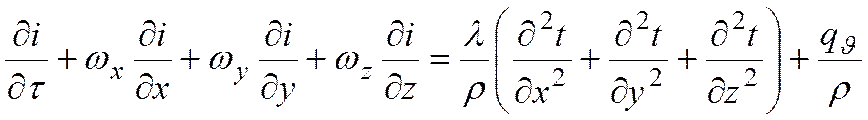

или, если ,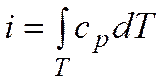

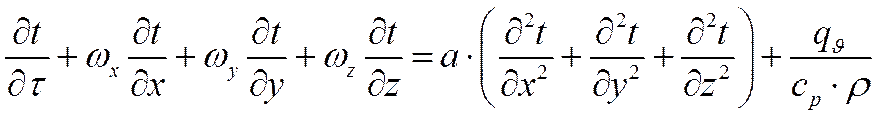
Последнее уравнение является уравнением энергии, описывающим распределение температур внутри движущейся жидкости.

Если 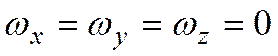, уравнение энергии переходит в уравнение теплопроводности.

Как следует из уравнения энергии, темпера­турное поле в движущейся жидкости зависит от составляющих скорости .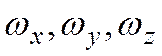

Чтобы сде­лать систему уравнений замкнутой, необходимо добавить уравнения, которые бы описывали из­менение скорости во времени и пространстве. Такими уравнениями являются дифференциаль­ные уравнения движения.

Уравнения движения.

Уравнение движения вдоль оси Ох

.

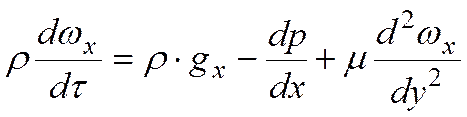Описание движения жидкости усложняется, если скорость изменя­ется по трем направлениям.

для оси Ох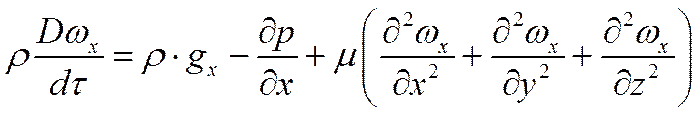

для оси Оу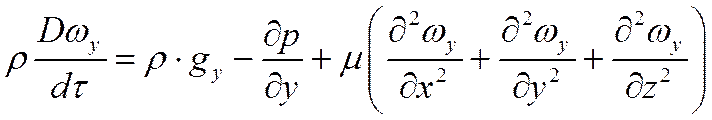

для оси Оz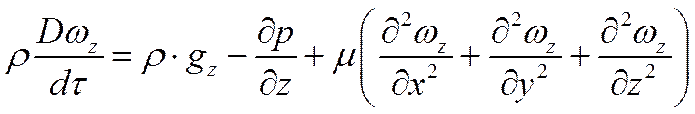

В общем случае составляющие скорости 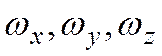изменяются во времени и в пространстве. Член, стоящий в левой части уравнений, представляет собой полную производную от скорости по времени.

На основании понятия о полной (субстанциальной) производной для оси Ох имеем

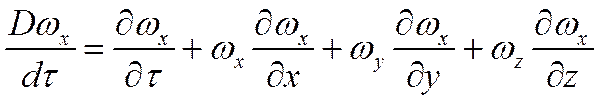
Аналогичные уравнения можно записать и для осей Оу, Оz.

Используя векторную форму записи:

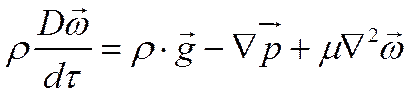
Уравнение движения получено без учета зависимости физи­ческих параметров жидкости от температуры. В частности, не учтена зависимость плотности от температуры.

В то же время свободное дви­жение жидкости определяется разностью плотностей холодных и нагре­тых частиц жидкости.

Приближенный учет переменности плотности возможен с введением температурного коэффициента объемного расши­рения β.

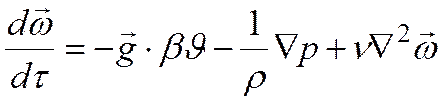
Т.к. в уравнение движения, помимо 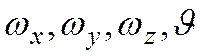входит еще неизвестная величина р, то система уравнений не является замкнутой. Необходимо добавить еще одно уравнение – уравнение сплошности (неразрывности).

Уравнение сплошности.

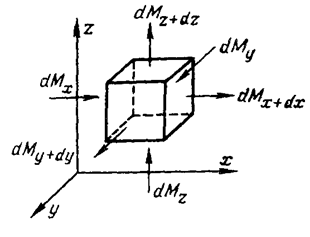Выде­лим в потоке движущейся жидкости непо­движный элементарный параллелепипед со сторонами dx, dy и dz и подсчитаем массу жидкости, протекающей через него в на­правлении осей Ох, Оу и Oz за время dτ.

В направлении оси Ох в параллелепи­пед втекает масса жидкости

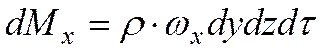
Величина 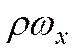представляет собой ко­личество массы, протекающей в единицу времени через единицу поперечного сече­ния. Из противоположной грани вытекает масса

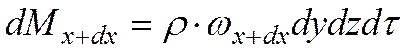
Ограничиваясь первыми двумя членами разложения в ряд, полу­чаем, что масса dM_x+dx, вытекающая из элементарного параллелепида в направлении оси Ох

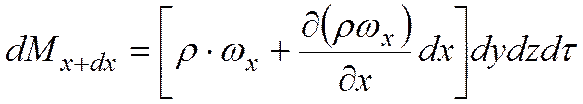
Излишек массы жидкости, вытекающий из элементарного объема в направлении оси Ох

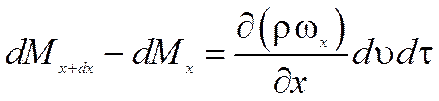
Аналогичным образом можно получить уравнения для направлений по осям Оу и Оz.

Полный избыток мас­сы жидкости, вытекающей из элементарного объема в направлении всех трех осей обусловливается измене­нием плотности жидкости в объеме dυ и равен изменению массы дан­ного объема во времени .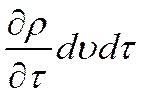

Произведя сокращение на dυ и dτ и перенеся все члены в левую часть равенства, окончательно получим дифференциальное уравнение сплошности для сжимаемых жидкостей

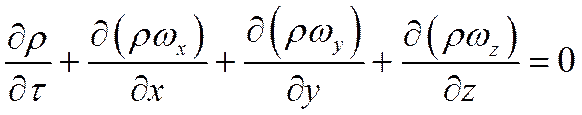
Для несжимаемых жидкостей, полагая ρ=const, получаем

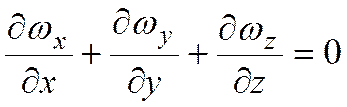
Уравнение сплошности является уравнением сохранения массы.