Критерии подобия и уравнения подобия

Подобие процессов конвективного теплообмена

Конвективный теплообмен описывается системой дифференциальных уравнений и условиями однозначности с большим количеством перемен­ных. Аналитическое решение полной системы уравнений на­талкивается на серьезные трудности.

Поэтому большое значение при­обретает экспериментальный путь исследования. С помощью экспери­мента для определенных значений аргументов можно получить числовые значения искомых переменных и затем подобрать уравнения, описываю­щие результаты опытов.

Однако для исследования влияния на процесс какой-либо одной величины остальные нужно сохранять неизменными, что не всегда возможно из-за большого количества переменных.

Кроме того, при этом нужно быть уверенным, что результаты, получаемые с помощью какой-либо конкретной установки (модели), можно перенести и на дру­гие аналогичные процессы (образец).

Эти трудности помогает разрешить теория подобия.

С помощью теории подобия размерные физические ве­личины можно объединить в безразмерные комплексы, причем так, что число комплексов будет меньше числа величин, из которых составлены эти комплексы. Полученные безразмерные комплексы можно рассма­тривать как новые переменные.

При введении в уравнения безразмерных комплексов число величин под знаком искомой функции формально сокращается, что упрощает исследование физических процессов.

Кроме того, новые безразмерные переменные отражают влияние не только отдельных факторов, но и их совокупности, что позволяет легче определить физические связи в ис­следуемом процессе.

Для практического использования выводов теории подобия необхо­димо уметь приводить к безразмерному виду математические описания изучаемых процессов.

Критерии подобия и уравнения подобия

Помимо безразмерных величин 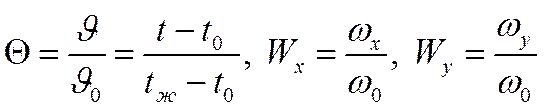и безразмерных координат 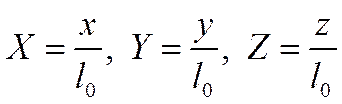, в уравнения конвективного теплообмена входят также безразмерные комплексы, состоящие из разнородных физических величин

.

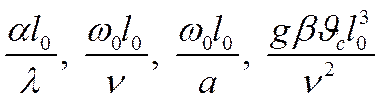Этим комплексам, называемым числами подобия, присвоены имена ученых, внесших значительный вклад в развитие теплотехники и механики.

Первый из этих безразмерных комплексов обозначают

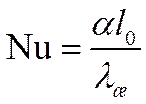
и называют числом Нуссельта или безразмерным коэффициентом теплоотдачи.

Число Нуссельта характеризует теплообмен на границе стенка/жидкость. В задачах конвективного теплообмена число Nu обычно является искомой величи­ной, поскольку в него входит определяемая величина α.

Безразмерный комплекс

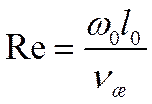
называют числом Рейнольдса. Оно характеризует соотношение сил инерции и сил вязкости.

Третий безразмерный комплекс обозначают

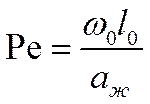
и называют числом Пекле.

Его можно преобразовать следующим образом

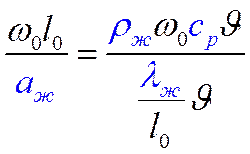
здесь числитель характеризует теплоту, переносимую конвекцией, а знаменатель – теплоту, переносимую теплопроводностью.

Безразмерный комплекс

называют числом Грасгофа. Оно характеризует подъемную силу, возникающую в жидкости вследствие разности плотностей.

Т.к. при выводе уравнения движения было принято 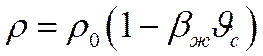-> 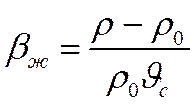, то вместо Gr можно написать его общую модификацию – число Архимеда

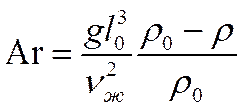
В случае однородной среды при условии β=const число Архимеда идентично числу Gr.

Безразмерные величины Θ, W_х, W_y, X, Y, Nu, Re, Ре, Gr можно рас­сматривать как новые переменные. Их можно разделить на три группы:

- независимые переменные – это безразмерные координаты X, У;

- зависимые переменные – это Nu, Θ, W_x, W_y;

- постоянные величины – это Ре, Re, Gr; они заданы условиями однозначности и для конкретной задачи являются постоянными.

В результате можно написать

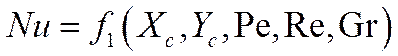
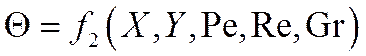
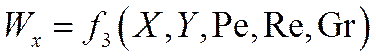
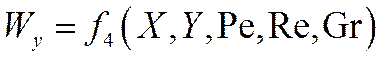
Здесь Х_с, Y_c соответствуют поверхности теп­лоотдачи (стенки).

Безразмерный комплекс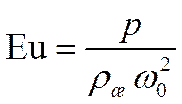

называют числом Эйлера. Это число характеризует соотношение сил давления и сил инерции.

В уравнения конвективного теплообмена зави­симая переменная Еu входит только под знаком производной. Следова­тельно, для несжимаемой жидкости с постоян­ными физическими параметрами существенно не абсолютное значение давления, а его изменение. Поэтому число Эйлера обычно представляют в виде

,

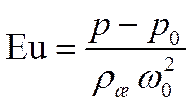где р₀ – какое-либо фиксированное значение давления, например давле­ние на входе в канал.

Очевидно, при неизменной математической формулировке задачи новые безразмерные величины могут быть получены комбинированием старых безразмерных величин.

Число Ре можно представить как произведение двух безразмерных переменных

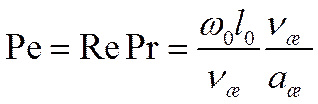
Безразмерная величина 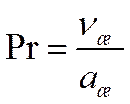представляет собой новую перемен­ную, называемую числом Прандтля. Число Прандтля целиком со­ставлено из физических параметров, и поэтому само является физи­ческим параметром. Его можно записать и в виде

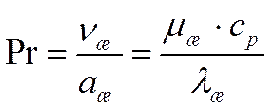
Числу Прандтля можно придать определенный физический смысл.

Уравнение энергии ,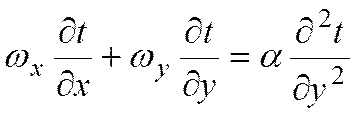

и уравнение движения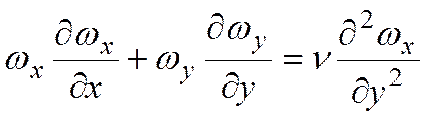

по записи аналогичны.

При 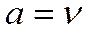расчетные поля температур и скоро­стей будут подобны, если только аналогичны и условия однозначности. Таким образом, при определенных условиях числу Прандтля может быть придан смысл меры подобия полей темпе­ратур и скоростей.

Безразмер­ные переменные можно разделить на два вида:

- определяемые – это числа, в которые входят искомые зависи­мые переменные; в рассматриваемом случае зависимыми являются 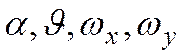, следовательно, определяемыми являются Nu, Θ, W_x и W_y;

- определяющие – это числа, целиком составленные из незави­симых переменных и постоянных величин, входящих в условия однознач­ности; в рассматриваемом случае определяющими являются X, У, Re, Pr (или Ре) и Gr.