Внутренняя задача тепломассообмена

Внутренняя задача тепломассообмена предполагает, что сопротивление переносу сосредоточено внутри частицы и изменением концентрации во внешнем потоке можно пренебречь.

Исследование внутренней задачи тепло- и массообмена можно провести на примере обтекания осесимметричным потоком капли на основании уравнения конвективного переноса полагая, что значения компонентов вектора скорости известны.

.

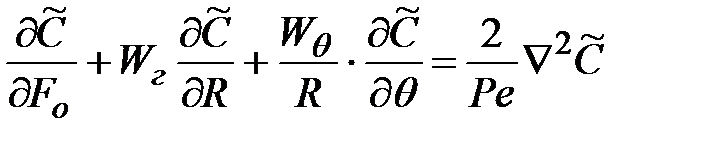Пусть в начальный момент времени концентрация растворенного в апле вещества постоянна по объему, тогда без ограничения общности краевые условия можно представить в виде

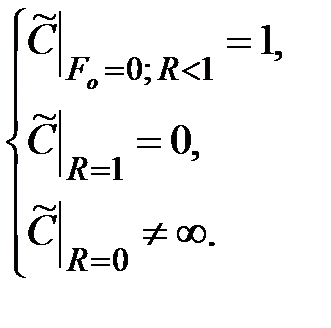(3.18)

Такая задача рассмотрена только для капли, движущейся при Ре>>1, когда известны точные значения компонентов вектора скорости жидкости внутри капли. В предельном случае Ре®0 массо- и теплоперенос описывается уравнением нестационарного молекулярного переноса, решение которого можно получить разделением переменных в уравнении Лапласа. Полученное Ньюменом выражение для средне концентрации вещества в частице имеет вид

.

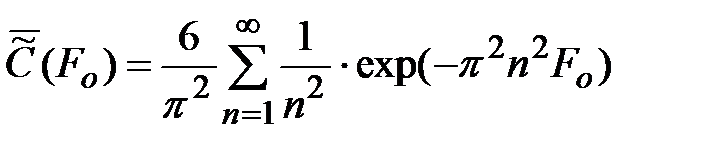Из формулы следует, что средняя концентрация вещества в капле уменьшается экспоненциально с течением времени (увеличение критерия F_o).

Выражение для средней концентрации вещества в капле имеет вид:

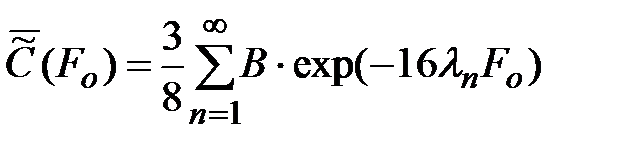, (3.19)

где B_n, l_n – численные коэффициенты.

При F_o®¥ ряд быстро сходится и можно ограничиться первым членом ряда. При F_o®0 ряд сходится крайне медленно и при малых значениях F_o обычно используют численные методы решения (3.2) с краевыми условиями (3.1).

Найдем среднее значение коэффициента массоотдачи. За dt количество экстрагируемого вещества . Эту же величину потока асссы можно выразить как

.

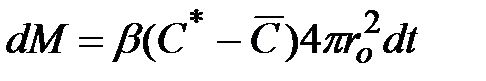Приравняв эти выражения, получим

.

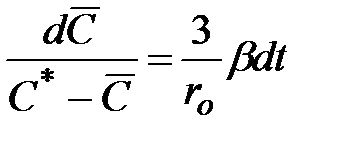Интегрируя это соотношение и вводя средний по времени коэффициент массоотдачи 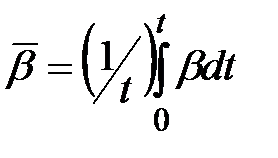, получ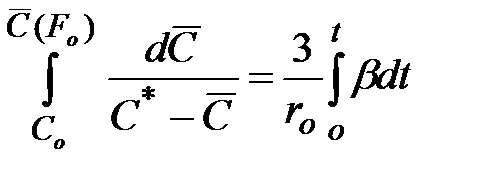или

или .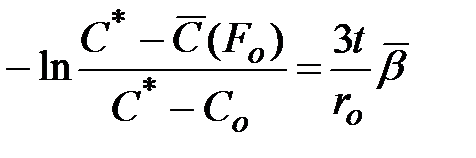

Используя величину степени извлечения А, последнее выражение можно представить в виде

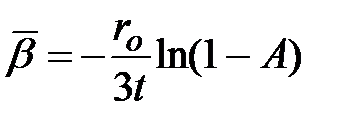. (3.20)

Учитывая, что диффузионный критерий Фурье имеет вид 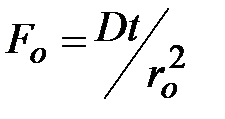и используя выражение (3.20), получили зависимость для среднего значения числа Шервуда

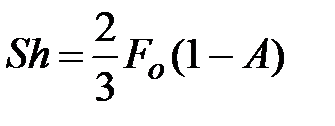. (3.21)