Измерение риска и методы его уменьшения
Когда цены и доходы слишком волатильны (быстро меняются), являются неопределенными, то возникает проблема потребительского выбора в условиях неопределенности и риска. При этом необходимо учитывать параметры риска, уметь оценивать степень риска в ситуации альтернативных вариантов, и, наконец, добиваться снижения риска и неопределенности. Изменчивость (волатильность) экономических величин, переменных, их неопределенность – главные причины экономического риска.
Измерение риска связано с определением вероятности события, вычислением ожидаемого значения результата и оценкой отклонений ожидаемых результатов от действительных величин.
Объективный метод определения вероятности основан на вычислении частоты, с которой происходят некоторые события. Вычисляется ожидаемое ее математическое значение – математическое ожидание Е(Х), которое равно сумме произведений числовых значений ожидаемых величин на их вероятности:
Е(Х)= 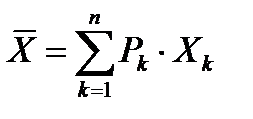 ,
,
где Рk – вероятность события k. 0< Рk <1; 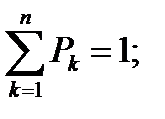
Хk – числовое значение события k.
Идея оценки риска через вероятность и его математическое ожидание принадлежит Н. Бернулли в его задаче о Санкт-Петербургском парадоксе о вероятности выпадения «орла» при подкидывании монеты n раз (1738г.).
Допустим, валютный трейдер ожидает через месяц обменный курс USD/RUR=28,40 с вероятностью 40%, 29,19 – с вероятностью 25%, 28,10 – с вероятностью 15%, 27,80 – с вероятностью 10% и 30,20 – с вероятностью тоже 10%. Какой курс наиболее вероятен?
Этот курс отпределим, вычисли математическое ожидание курса Е(Х)=28,70∙0,4+29,10∙0,25+28,10∙0,15+27,80∙0,1+30,20∙0,1=27,78.
Именно такой курс рациональный трейдер будет закладывать в свои решения по форвардной покупке или продаже долларов за рубли, сравнивая это математическое ожидание с форвардным рыночным месячным курсом. Например, если рыночный курс 28,40, то трейдер заключит форвардную сделку на покупку по этому курсу 1 млн. USD через месяц. Он ожидает получить прибыль в 38 коп. с каждого доллара, который он собирается продать по ожидаемому курсу 28,78. Ожидаемый доход от операции 380.000 рублей, а ее доходность 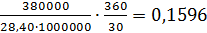 или 15,96% годовых.
или 15,96% годовых.
Конечно, вовсе не обязательно, что его ожидания оправдаются. Возможно, что все его субъективные оценки вероятностей неверны и тогда математическое ожидание, построенное на этих оценках, дает неверный ориентир.
Рациональным является такое поведение оператора (действующий экономический агент), когда он стремится принимать решение на основе математического ожидания. Но на практике нужно учитывать и субъективный (психологический) фактор – операторы часто предпочитают обеспечение надежности в области значений, близких к достоверности, а не ориентироваться на математическое ожидание (парадокс Алле, 1952 г.). Такое психологическое решение возможно, если оператор переоценивает вероятность события, например, в условиях контекста, когда окружающая обстановка заставляет поверить именно в этот исход, а не в математическое ожидание.
Для выбора альтернативного решения необходимо сопоставить отклонения между действительным результатом и ожиданиями. Чем больше отклонение от математического ожидания, тем больше риск. На практике обычно используют дисперсию – средневзвешенное (по вероятностям) из квадратов отклонений действительных результатов от ожидания D(х)=σ2= 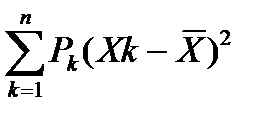 или стандартное отклонение (среднее квадратичное отклонение) равное
или стандартное отклонение (среднее квадратичное отклонение) равное 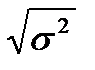 . Если вероятности событий (исходов) неизвестны, то формула дисперсии будет иметь вид:
. Если вероятности событий (исходов) неизвестны, то формула дисперсии будет иметь вид:
σ2=  .
.
Для большинства экономических процессов вероятности их результатов подчиняются нормальному закону распределения или кривой нормального распределения (кривой Гаусса). Для нормального распределения составлены таблицы значений функций вероятности отклонений и с их помощью можно обоснованно принимать решения по альтернативным вариантам. Например, в инвестиционном анализе, при управлении инвестиционными рисками. Если рассматривается инвестирование в тот или иной рискованный актив, то необходимо выяснить, какую максимальную сумму можно потерять. Составляется нормальное распределение вероятности различных результатов (прибылей и убытков) от таких инвестиций и по соответствующим таблицам находится коэффициент вероятности отрицательной доходности от капиталовложений (необходимая вероятность задается – 80%, 95%…).
Подсчеты средних величин, дисперсии, стандартного отклонения волатильности цен для измерения риска сегодня осуществляется с использованием электронных таблиц, пакетов программ статистической обработки (A-Pack: аналитический пакет для бизнеса, например) и специальных калькуляторов.
Рассмотрим выбор работы продавцом в двух разных местах с одинаковым ожидаемым доходом 1500 долл., причем на первом месте оплата (доход) зависит от объема продаж, а на втором – работа оплачивается по ставке. Имеется две разных возможности (вероятности на первом месте): 2000 долл. при хорошей распродаже (50% веротяности) и 1000 долл. при скромной. На втором месте также две возможности: за работу платят 1510 долл., а при закрытии магазина (1% вероятности) 510 долл. – выходное пособие. Оба места работы имеют действительно одинаковый ожидаемый доход в 1500 долл.:
0,5*2000+0,5*1000=0,99*1510+0,01*510=1500 (по формуле математического ожидания).
Какой вариант выбрать? Попробуем оценить риск по каждому варианту, по отклонению от ожидаемого результата:
| Место работы | Результат 1 | Отклонение | Результат 2 | Отклонение |
| Первое | ||||
| Второе |
Среднее отклонение по первому месту работы составит:
0,5*500-0,5*500=0.
Среднее отклонение по второму месту работы также составит:
0,99*10-0,01*990=0.
Следовательно, представляется, что оба места равноценны по риску. Однако, это не так. И это становится ясным, если рассмотреть не отклонения, а дисперсию σ2 и стандартное отклонение.
По первой работе σ2: 0,5*5002+0,5*5002=250000.
По второй работе σ2: 0,99*102+0,01*9902=9900.
Если используем стандартное отклонение 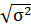 , то по первому варианту это равно 500, а по второму 99,6.
, то по первому варианту это равно 500, а по второму 99,6.
Следовательно первое место работы более рискованно, чем второе. Последнее обеспечивает более стабильный доход, а первое место весьма нестабильно по доходу (с 50% вероятностью колебание дохода в 2 раза).
Оценку риска финансовой деятельности компании или банка, а также вероятность их банкротства можно рассчитать по следующим формулам:
индекс риска 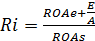 ,
,
где 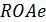 – ожидаемая рентабельность активов;
– ожидаемая рентабельность активов;
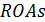 - стандартное отклонение рентабельность активов за период 5 лет;
- стандартное отклонение рентабельность активов за период 5 лет;
Е – собственный капитал компании (банка);
А – активы компании.
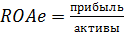 ;
;
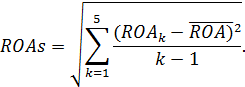
Вероятность банкротства компании (банка)= 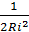 .
.
Сравним показатели финансовой деятельности Citigroup в 2000 г. и 2009 (пик мирового финансового кризиса).
В 2000 г. ожидаемая прибыль банка (π) 22 млрд. долл., а в 2009 г. – 2 млрд. Собственный капитал (Е) соответственно: 120 и 400 млрд; активы (А): 1884 и 2000 млрд. 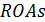 : 0,001 (0,1%) и 0,1 (10%).
: 0,001 (0,1%) и 0,1 (10%).
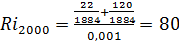 , и
, и 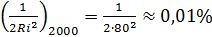 ;
;
 , и
, и 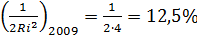 .
.
Видим, что в 200 году Ri=80 велик, а это означало очень низкую вероятность банкротства банка, а в 2009 году ситуация кардинально изменилась: Ri – мал, а вероятность банкротства вполне реальна. Такой же пример можно построить по финансовой отчетности «Дженерал Моторс» или JP Морган, которые в связи с мировым финансовым кризисом попали в предбанкротное состояние и вынуждены были с помощью правительства США принимать экстренные меры по спасению компаний.
Обращаем внимание на ключевое значение показателя 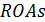 , т.е. стандартного отклонения рентабельности. Его увеличение означает нестабильную работу компании и нарастающий риск банкротства.
, т.е. стандартного отклонения рентабельности. Его увеличение означает нестабильную работу компании и нарастающий риск банкротства.
Снижение риска достигается, во-первых, путем диверсификации, т.е. увеличения альтернатив, увеличением количества благ или услуг с разной степенью риска. Это уменьшает дисперсию. Во-вторых, снижает риск страхование, которое перекладывает потери от рисков на страховщика за определенную плату – страховую премию. Аналогично страхованию является процедура предоставления гарантий третьих лиц или залогов имущества, ценных бумаг. В-третьих, уменьшается риск при получении более полной информации. В-четвертых, снижение рисков связано со специальными действиями по взаимно компенсирующим сделкам – хеджированием (операции с куплей-продажей разных товаров, фьючерсы и опционы по финансовым и валютным сделкам с разными ценными бумагами и валютами). Наконец, в-пятых, риск снижается путем создания резервов. Это исключительно важно для банков и регуляторы (центральные банки) требуют, особенно после мирового финансового кризиса 2007-2011 гг., чтобы против каждого кредита коммерческие банки образовывали резерв, увеличивали свой капитал не менее чем на 10% (а иногда на 100%, т.е. полностью устраняя риск невозвращения кредита).
В инвестиционной деятельности широко используется диверсификация портфеля активов инвестора, когда активы, т.е. средства, обеспечивающие их владельцу доходы, помещаются (инвестируются) в акции разных компаний, в разные облигации, в разные виды валюты, чтобы снизить риски потерь от неблагоприятных изменений цен (курсов). Здесь работает принцип: «не храни все яйца в одной корзине». Рисковые активы могут быть более прибыльными, но вероятность их обесценения конечно большая, чем у безрисковых, но менее доходных (государственных долгосрочных облигаций, например).
Пример хеджирования. Европейский импортер заключил выгодную сделку на ввоз в нашу страну медикаментов из ЕС со сроком оплаты в Евро через три месяца. Он опасается неблагоприятной динамики курса EUR/RUR. Если курс рубля упадет (т.е. EUR/RUR повысится с 39,50 до 40,20), то покупка Евро для погашения экспортного кредита по 40,20 принесет импортеру убыток.
Чтобы его уменьшить, импортер хеджирует риск путем проведения параллельной сделки: закрывает открытую рисковую позицию на «продажу» Евро экспортеру противоположной позицией – покупкой. Он одновременно со сделкой на покупку лекарств покупает фьючерсный контракт на покупку на бирже через три месяца по курсу 39,80 необходимого количества Евро. Если курс через три месяца выше 39,80, то импортер как покупатель товара будет нести потери, но как покупатель фьючерса получит выигрыш. Очень важно, что будет снят риск неопределенности валютного курса через три месяца.
Дата добавления: 2015-11-26; просмотров: 1673;
