Модель коробки Эджуорта
| I |
| QAI |
| II |
| H |
| QBI |
| F |
| QВII |
| QАII |
| K |
| M |
| N |
| Рис. 32. Коробка Эджуорта |
Рассмотрим ситуацию обмена благами А и В между потребителями I и II. Объединим на одном графике кривые безразличия I и II.
Фигура, которая заштрихована и ограничена исходными кривыми безразличия, представляет так называемое ядро – множество точек, характеризующих наборы благ А и В. В пределах ядра возможны паретоулучшения, т.е. повышение благосостояния I и II потребителей. Действительно, распределение благ А и В в точке К для них предпочтительнее, чем в точке Н – обеспечивает большую полезность. Ядро является областью взаимовыгодных сделок обмена благами между потребителями.
В точке касания М двух кривых безразличия потребителей I и II достигается состояние паретоэффективности (паретооптимальности): невозможно улучшить благосостояние одного потребителя, не ухудшив благосостояние другого. В этой точке обе кривые безразличия имеют одинаковый наклон относительно своих осей координат, а так как наклон кривых безразличия характеризует предельную норму замещения благ MRS, то условие паретоэффективности – это равенство у обоих потребителей предельных норм замещения потребляемых благ: MRSABI= MRSABII .
Все точки касания кривых в коробке Эджуорта, которая и выступает ядром, образуют множество паретоэффективных состояний в обмене в виде контрактной линии FMN. Можно, построить кривую потребительских возможностей двух потребителей, точки которой соответствуют величинам полезности потребителей в точках паретоэффективности на контрактной линии.
Задачи, связанные с потребительским выбором многих лиц по многим благам, рассматриваются в рамках теории игр при рассмотрении аксиоматических торгов, решающий вклад в которую был сделан в 40-50-е годы ХХ века экономистами-математиками Д. Нейманом, О. Моргенштерном, Д. Нэшем. Так, Д. Нэш доказал, что при выполнении ряда условий (аксиом) в задаче торга можно найти единственное справедливое решение, дающее ожидаемый каждым игроком выигрыш (увеличение полезности). Но важным является критерий справедливости. Например, в известном примере дележа продуктов два агента получают общий подарок, состоящий из одного литра джина и одного литра виски. Они должны справедливо поделить подарок между собой, учитывая, что второй агент не любит джин, а первый – одинаково любит и джин, и виски. Обычный эгалитаризм отдаст весь джин первому агенту, а все виски, второму. При этом очевидно, что будет ущемлен первый агент, потолок полезности которого равен двум единицам, а для второго равен только одной единице. Можно вычислить, что более справедливым будет решение по выделению первому агенту литра джина и 1/3 литра виски, а второму – 2/3 литра виски.
Рассмотрим дележ между Ивановым и Петровым 20 кг яблок и 30 кг груш. Функция полезности Иванова U(x,y)=xy, а функция полезности Петрова U(x,y)=xy2, где х – количество (кг) яблок; у – количество (кг) груш. Необходимо построить кривую контрактов и кривую потребительских возможностей. Кривую контрактов нужно строить по точкам паретооптимальных наборов, которые определяются из условий равенства предельных норм замены яблок грушами у Иванова и у Петрова.
Если – х1 и у1 количество яблок у Иванова, а х2 и у2 у Петрова, то условие равенства MRSхуи= MRSхуп :  (дифференцируем функции полезности по Х и по У и делим полученные значения).
(дифференцируем функции полезности по Х и по У и делим полученные значения).
Учитывая, что х1+х2=20 и у1+у2=30, получим, что 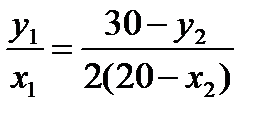 .
.
Задавая значения х1 от 0 до 20, получим значения остальных переменных, характеризующих точки кривой контрактов.
Пусть х1 последовательно равна 5, 10, 15, тогда для
точки А х1=5; х2=15; у1=30/7; у2=180/7;
точки В х1=10; х2=10; у1=10; у2=20;
точки С х1=15; х2=5; у1=18; у2=12.
Соединяя точки А, В, С и начало координат коробки Эджуорта, получим кривую контрактов (рис. 33):
| Рис. 33. Кривая контрактов |
| А |
| В |
| С |
| О Иванов |
| Y |
| О Петров |
| H |
| X |
Зная три варианта оптимального распределения яблок и груш, найдем уравнение полезности Иванова и Петрова в этих комбинациях и построим линию потребительских возможностей (рис. 34):
| Полезность Иванова |
| Полезность Петрова |
| 21,42 |
| А |
| В |
| С |
| А: полезность Иванова ≈ 21,42 полезность Петрова ≈ 9918 В: полезность Иванова ≈ 100 полезность Петрова ≈ 4000 С: полезность Иванова ≈ 270 полезность Петрова ≈ 720 |
| Рис. 34. Линия потребительских возможностей |
Вопросы для контроля и задания
1. Для двух потребителей товары Х и У являются совершенными заменителями в пропорции 1:1. Общее количество товара Х – 10 шт., У – 20 шт. Первоначальное распределение таково, что первому потребителю досталось 8 единиц Х и 3 единицы У. Является ли это распределение парето-эффективным?
2. Для двух потребителей товары Х и У являются взаимодополняющими в пропорции 1:1. Количество товаров Х=20 шт., У=20 шт. Нарисуйте линию кривой контрактов.
3. Функции полезности двух потребителей, участвующих в распределении благ Х и Y задаются формулами: U1=xy и U2=x+y. общее количество x=10, y=20, а цены Px=2, Py=3. Распределение благ следующее:
первый потребитель x=5 и y=12;
второй потребитель x=5 и y=8.
Определите: будет ли такое распределение оптимальным по Парето?
Дата добавления: 2015-11-26; просмотров: 2412;
