Особенности микроэкономического анализа производства. Производственная функция
Используем положения предельного анализа производства к фирме, работающей в условиях совершенной конкуренции (доступ на рынок не ограничен; продавцы принимают рыночные цены как данные и не влияют на них; всем доступна полная информация). Основные положения этого анализа:
1. Производство – это взаимодействие факторов (ресурсов), которое может быть описано соответствующей производственной функцией Q=ƒ(x1,x2,…xi,…xn), где Q – объем производства (количество продукции), xi – затраты (количество) i-го фактора.
К факторам относятся земля и природные ресурсы (N), труд (L), капитал (К), организация и управление, знания и опыт.
2. Фирма решает оптимизационную задачу: как с помощью заданных ресурсов максимизировать свою полезность, обеспечить наибольший объем выпуска и объем продаж и получить максимальную прибыль.
3. Взаимозаменяемость факторов приводит к альтернативным вариантам производства и к различному их выбору.
4. Производственную деятельность фирмы следует рассматривать в коротком периоде (SR – shot run), когда не изменяется структура факторов и отсутствуют инвестиции, и в долговременном периоде (LR – long run), когда осуществляются инвестиции и меняется структура и количество факторов.
Краткосрочная производственная функция показывает выработку Q, которую фирма достигает, изменяя ресурсы. Если все факторы используются полностью, т.е. фирма реализует в максимальной мере свой потенциал, то эта ситуация иллюстрируется с помощью линии производственных возможностей (ЛПВ). Движение по этой линии отражает переход от одних вариантов использования ресурсов к альтернативным. Например, завод, используя все свои мощности и рабочую силу, может производить разное количество танков и тракторов и, наращивая производство тракторов вместо танков (конверсия) он переходит из А в В на ЛПВ предприятия (рис. 35):
| • A |
| • B |
| • D |
| Танки |
| Тракторы |
| • C |
| THA |
| THB |
| TPA |
| TPB |
| Рис. 35. Линия производственных возможностей |
Производство танков сокращается на (ТНА-ТНВ), а производство тракторов увеличивается на (ТРВ-ТРА) при полном использовании наличных ресурсов.
Если выпуск продукции завода соответствует точке С, то это означает, что производственный потенциал недоиспользуется и предприятие работает неэффективно. Ситуация Д при имеющихся ресурсах недостижима, она находится уже на более высокой ЛПВ.
Предельный анализ производственной функции позволяет определить предельный продукт, средний продукт, предельную производительность.
Предельный продукт МР характеризует величину изменения выработки ΔQ при использовании дополнительной единицы ресурса (рабочей силы, капитала, земли…): 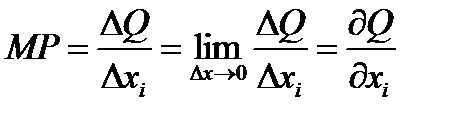 .
.
Предельный доход по фактору (ресурсу) MRx – это денежная величина предельного продукта данного фактора. Он равен произведению цены продукта Р на МР, т.е. p*(dQ/dx). Эту величину нужно отличать от предельного дохода как предельной выручки MR, который показывает степень изменения совокупной выручки (TR=P*Q) при изменении выпущенной и проданной продукции: 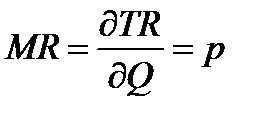 .
.
Средний продукт АР – это средняя выработка на единицу ресурса: АР= Q/ xi.
МР и АР характеризуют предельную и среднюю производительность (отдачу) по данному ресурсу (фактору). Наиболее часто используется предельная и средняя производительность труда: выработка на одного дополнительного работника и средняя выработка.
Практическое значение имеют два правила минимизации издержек и максимизации дохода фирмы:
1. Минимальная сумма издержек фирмы достигается тогда, когда равны предельные продукты, деленные на цену соответствующих факторов:

2. Максимальный доход фирма-производитель обеспечивает тогда, когда предельные продукты факторов i в денежном выражении равны ценам Pi соответствующих факторов:
MPi=Pi
Если последовательно увеличивать затраты какого-то одного фактора, а затраты других факторов не изменять, то будет наблюдаться сокращение предельного продукта. Эта важнейшая закономерность (принцип) убывающей предельной производительности факторов подтверждается эмпирически. Однако, нужно учитывать, что начинает действовать эта закономерность только после достижения определенного уровня затрат данного фактора и если другие факторы не изменяются.
| AP |
| X |
| Q |
| Q, MP, AP |
| MP |
| I |
| II |
| III |
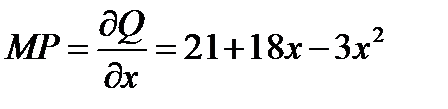 ;
AP=Q/x=21+9x-x2 . ;
AP=Q/x=21+9x-x2 .
|
| Рис. 36. Принцип убывающей предельной производительности |
Видны три стадии производства:
I когда 0<x<4,5. Выработка быстро растет, АР растет и МР>АР. На этой стадии ресурсы недоиспользуются.
II 4,5<x<7. Рост выработки замедляется и доходит до максимума, МР уменьшается до 0, АР доходит до максимума и везде превышает МР. Эта стадия оптимальной эффективности производства.
III х>7. Выработка уменьшается, падает АР, а МР<0. Эта стадия неэффективного производства в краткосрочном периоде.
Если изменяются все факторы, то возникает проблема отдачи от масштаба – воздействие пропорционального изменения количества факторов на объем выпуска продукции фирмы.
Различают постоянную отдачу от масштаба, когда увеличение (уменьшение) количества всех факторов в n раз увеличивает (уменьшает) выработку в n раз: ƒ(nxi)=nQ.
Возрастающая отдача означает, что увеличение всех факторов в n раз увеличивает выпуск в kn раз, где k>1: ƒ(nxi)=knQ.
Убывающая отдача: увеличение факторов в n раз увеличивает выпуск только в mn раз, где m<1. Ярким примером убывающей отдачи был завод Форда в Ривер Руж, на котором работало 75000 рабочих и где был развернут весь комплекс производства от стали, литья и проката до сборки автомобилей. Но завод оказался нерентабельным, плохо управляемым и скоро был закрыт. Убывающая отдача была характерна и советским гигантским машиностроительным заводам («Уралмаш», Кировский и др.).
Связь между ростом выработки и изменением затрат ресурсов найдена эмпирически и описывается законом опыта и кривой опыта (обучения): при каждом удвоении выпуска продукции затраты ресурсов на 1 единицу стандартной продукции уменьшаются на определенную величину, на определенный фиксированный процент (автомобилестроение в США –12%, самолетостроение и сталелитейные производства – 30%, производство полупроводников – 40%). Бостонская консалтинговая группа (BCG) в 70-е годы ХХ века даже рассчитала формулу зависимости новых издержек С от первоначальных (С0) и от изменения выпуска продукции с Q0 до Q:
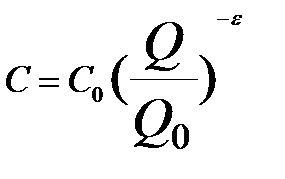 , где ε – коэффициент эластичности выпуска по издержкам.
, где ε – коэффициент эластичности выпуска по издержкам.
| 60% кривая опыта |
| 70% кривая опыта |
| С (в%) |
| Выпуск |
| 70% |
| Рис. 37. Кривая опыта |
Феномен кривой опыта объясняется тем, что при наращивании выпуска рабочие обучаются в процессе повторяемости операций, отрабатывается и «доводится» технология, меньше становится потерь и остановок производственного процесса.
Кривая опыта широко используется в стратегическом менеджменте.
Наибольший практический интерес вызывает производственная функция, связывающая выпуск, труд и капитал: Q=ƒ(L,K).
Такую функцию еще в 1920-е годы исследовали экономист П. Дуглас и математик Д. Кобб. Производственная функция Кобба-Дугласа, полученная на обобщенных данных американской экономики, имела вид:
Q=A*LαKβ, где А – const, α, β – коэффициенты эластичности выпуска продукции по труду и капиталу, показывающие процентное изменение выпуска при однопроцентном изменении затрат труда или капитала.
В классической функции Кобба-Дугласа α<1, β<1, а сумма α +β = 1, т.е. имеется ситуация постоянной отдачи от масштаба (например, для американской экономики 20-50-х годов эта функция имела вид Q=1.01*L3/4*K1/4, т.е. фактор труд оказывал на выпуск продукции в три раза большее воздействие, чем капитал). Но вполне возможна ситуация, когда α + β > 1 – это возрастающая отдача от масштаба или α + β < 1 – это убывающая отдача от масштаба.
При постоянной отдаче, когда β=1-α, производственную функцию Кобба-Дугласа можно записать в дифференциальной форме (это вытекает из теоремы Эйлера о разложении прироста функции на доли прироста аргументов-факторов): 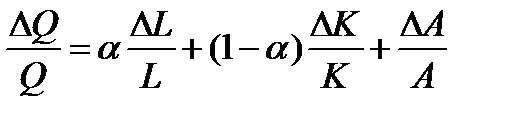 .
.
Отсюда видим, что темп роста производства (ΔQ/Q) равен сумме темпа роста труда (вклад труда), темпа роста капитала (вклад капитала) и темпа роста, связанного с изменением технологии, ростом опыта и знаний (вклад так называемого «остатка Солоу»).
Производственные функции, которые рассматривает экономическая теория, нужно отличать от производственно-технологических функций, которые не учитывают отдачу от масштаба, цены факторов. В сельском хозяйстве известна, например, производственно-технологическая функция Хеди, связывающая урожай и вносимые минеральные удобрения: Q=-5,68-0,316N-0,417P+0,6312 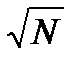 +8,5155
+8,5155 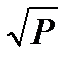 +0.3410
+0.3410 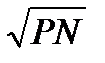 , где Q – урожай зерна в бушелях с акра; N – фунты азота, P – фунты фосфора.
, где Q – урожай зерна в бушелях с акра; N – фунты азота, P – фунты фосфора.
Дата добавления: 2015-11-26; просмотров: 1161;
