Кривые безразличия и бюджетные ограничения
Ординалистский подход обходит очень сложную проблему исчисления полезности (во многом субъективную) и устанавливает лишь порядковую полезность. На этой основе также можно решать вопрос о максимизации набора. Для этого применяется аппарат кривых безразличия (Ф. Эджуорт, 1881 г. и В. Парето, 1906 г.)
| Рис. 18. Построение кривых безразличия
|
Пусть решается задача о выборе наилучшего потребительского набора из двух благ. (Это довольно общая задача, так как можно представить, что выбирают из какого-то данного блага и суммой всех остальных благ). Построим график функции Г полезности двух переменных благ X1 и Х2. Это будет поверхность (при n переменных – гиперповерхность порядка n+1). Для определения величины полезности U1, U2, … нужно построить на плоскости X1OX2 линии одного уровня полезности путем проецирования на эту плоскость следов параллельного сечения поверхности Г, проходящего через координаты U1, U2… (рис. 18).
Эти линии одного уровня полезности U1, U2…. называются потребительскими изоквантами или кривыми безразличия.
Кривая безразличия представляет геометрическое место точек, отражающих равновыгодные для потребителя (с точки зрения полезности) наборы из двух благ.
Предположим, что потребителю безразлична конкретная комбинация набора, так как их полезности одинаковы. Например, потребитель выбирает разное количество единиц одежды и продовольствия, причем их суммарная полезность в каждом наборе одинакова (табл. 4):
Таблица 4. Наборы равной полезности
| Набор
| a
| b
| c
| d
| e
| f
|
| Одежда (ед.)
|
|
|
|
|
|
|
| Продовольствие (ед.)
|
|
|
|
|
|
|
Ua=Ub=Uc=Ud=Ue=Uf – полезности наборов равны.
| Рис. 19. Кривая безразличия
|
График кривой безразличия abcdef (рис. 19):
| Рис.20. Карта кривых безразличия
|
Для разных значений (уровней) U функции полезности Г можно составить карту кривых безразличия (рис. 20):
Кривые безразличия обладают рядом свойств:
1) каждому значению полезности Ui соответствует только одна линия безразличия. Отсюда – кривые безразличия не могут пересекаться.
2) Кривые безразличия имеют отрицательный наклон и вогнуты к началу координат, так как уменьшение количества одного товара и полезности от него должно быть компенсировано приростом полезности и количества другого блага, чтобы сохранить общую величину полезности.
3) Угол наклона кривой безразличия характеризует предельную норму замещения (MRS) одного блага другим. Кривая безразличия – это кривая взаимозаменяемости благ. MRS показывает, от какого количества товара X2 потребитель готов отказаться, чтобы получить дополнительную единицу товара X1 (рис. 21).
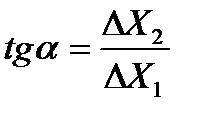 ; ;  ; ; 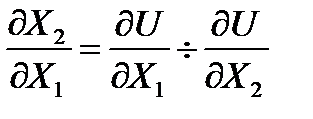 , т.е. предельная норма замещения равна обратному соотношению предельных полезностей благ. , т.е. предельная норма замещения равна обратному соотношению предельных полезностей благ.
|
| Рис.21. Предельная норма замещения
|
Наклон кривой безразличия и MRS можно использовать для иллюстрации потребительских предпочтений (см. пример в вопросах для контроля).
Кривые безразличия – не обязательно гиперболы. Для товаров, являющихся совершенными заменителями, кривая безразличия становится прямой с углом наклона 45о, поскольку потребитель всегда готов отдать одну 1 единицу блага Х1 в обмен на одну единицу блага Х2 (рис. 22 а). Ситуация взаимодополняющих товаров изображается кривой безразличия, состоящей из соединяющихся вертикального и горизонтального отрезков (ее иногда называют L-образная кривая безразличия). В данном случае, для потребителя интерес представляет только определенная комбинация благ (точка С на рис. 22 б), увеличение потребления любого из них не приносит большей полезности по сравнению с данной комбинацией (классический пример здесь – правый и левый ботинок).
| Рис. 22 а. Кривая безразличия
товаров-заменителей
|
| Рис. 22 б. Кривая безразличия
товаров-дополнителей
|
После рассмотрения заменяемости благ перейдем к проблеме выбора в условиях ограниченных возможностей потребителя, что связано с ценами благ и его доходом. Бюджетное ограничение показывает все комбинации (наборы) товаров, которые потребитель может приобрести при данном его доходе M и ценах соответствующих благ Pi. В общем виде модель поведения потребителя можно представить в виде:
существующие разные наборы благ: X=X1,X2,…Xn;
цены товаров: P=P1,P2,…Pn;
доход потребителя:M;
бюджетное ограничение:  ;
;
необходимо максимизировать полезность набора: max U(X).
В теории показывается, что искомый набор X*=x1*, x2*, x3*,…xn* можно определить. Покажем это на простом примере нахождения оптимального набора из двух товаров X1 и X2 с ценами P1 и P2 для потребителя с доходом М.
Бюджетное ограничение в этом случае имеет вид: P1*X1+P2*X2 = М.
Это уравнение прямой, пересекающей оси и X1 и X2 в точках М/P1 и М/P2 и представляющей линию цен с отрицательным наклоном:  (рис. 23).
(рис. 23).
Если изменяются цены и их соотношение, то изменяется наклон бюджетного ограничения. Если соотношение цен не изменяется, а изменяется доход (бюджет) М, тогда будет передвигаться (параллельный перенос) линия бюджетного ограничения.
Точка касания (Е) данного бюджетного ограничения с соответствующей кривой безразличия, характеризует параметры (X1Е и X2Е) набора двух благ с максимальной полезностью при заданном доходе (рис. 24):
| Рис. 23. Линия бюджетного ограничения
|
| Рис. 24. Точка оптимума потребителя
|
Бюджетная линия – геометрическое место точек комбинаций наборов с разными полезностями. Максимальная полезность для этой линии будет достигнута в точке Е, через нее проходит самая высокая кривая безразличия. Это точка оптимального потребительского выбора, точка «равновесия потребителя».
В точке Е tg угла наклона бюджетной линии равен –P1/P2 и равен tg угла кривой безразличия, т.е. MRS. Отсюда: предельная норма замещения (MRS) благ в точке оптимального потребительского выбора равна обратному соотношению цен этих благ. Но так как MRS равна обратному соотношению предельных полезностей благ, то это соотношение предельных полезностей равняется соотношению цен потребляемых благ: 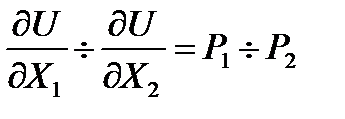 ,
,  отсюда
отсюда 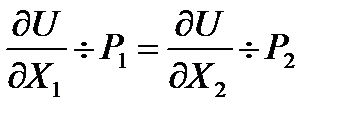 , т.е. мы пришли к эквамаржинальному принципу, по которому рациональный потребитель распределяет свой денежный доход таким образом, чтобы предельные полезности приобретаемых им благ, отнесенные к цене этих благ, были равными.
, т.е. мы пришли к эквамаржинальному принципу, по которому рациональный потребитель распределяет свой денежный доход таким образом, чтобы предельные полезности приобретаемых им благ, отнесенные к цене этих благ, были равными.
В инвестиционном анализе базовой является теория выбора оптимального портфеля Г.Марковица (1952г.), в которой используется метод касания кривых безразличия, описывающих отношения инвестора к риску и доходности ценных бумаг, с «бюджетным ограничением», характеризующим «эффективное множество» портфелей. Портфель инвестора включает множество комбинаций наборов ценных бумаг, но эффективным из них будет множество, удовлетворяющее двум условиям: а) обеспечение максимальной ожидаемой доходности для некоторого уровня риска; б) минимальный риск для определения значения ожиданий доходности.
Оптимальным будет такой портфель О*, который соответствует точке касания кривой безразличия I2 и эффективного множества (рис. 25).
| Эффективное множество портфелей
|
| Рис. 25. Оптимальный портфель инвестора
|
| Рис. 26 а. Кривая «доход-потребление»
|
Если соединить все точки равновесия потребителя при росте его дохода, то получим кривую «доход-потребление» (OY), которая показывает, как количество купленного товара связано с доходом потребителя (рис. 26 а):
С ростом дохода кривая «доход-потребление» прижимается к оси Х2, что означает предпочтение при высоких доходах товара Х2 (качественный товар) по сравнению с товаром Х1 (некачественный товар).
Однако реальный доход возрастает не только в том случае, если потребитель начинает больше зарабатывать. Он возрастает и тогда, когда снижаются цены. В результате на то же количество денег можно купить больше, чем прежде. Если относительные цены двух благ остаются неизменными, то снижение цен влияет на бюджетную линию точно так же, как и увеличение дохода, - она сдвигается вправо параллельно самой себе.
Если меняется цена блага Х1 или блага Х2, то бюджетная линия сдвигается вправо (или влево) вдоль одной из осей. Пусть, например, цена блага Х1 снижается, а цена блага Х2 остается неизменной. Тогда бюджетная линия смещается вправо вдоль оси абсцисс, а ее соединение с осью ординат остается на прежнем месте. Если бы менялась цена блага Х2, а цена блага Х1 не менялась, то соединение бюджетной линии с осью абсцисс оставалось бы на прежнем месте, тогда как ее соединение с осью ординат сдвигалось в направлении (вверх или вниз), обратном изменению цены.
| Рис. 26 б. Кривая «цена-потребление»
|
Если соединить все точки равновесия потребителя в данном случае, то получим кривую «цена-потребление» (OY), которая показывает, как меняется оптимальное потребление двух благ в результате изменения цены одного из благ (при предположении о неизменности дохода и цены другого блага) (рис. 26 б):
Интересны также кривые Энгеля[7], которые появились в конце XIX века и характеризовали влияние изменения дохода на структуру потребительских расходов. Например, для продовольствия и товаров первой необходимости с ростом дохода потребление растет медленнее (рис. 27 а), чем для качественных товаров, услуг и большинства промышленных товаров (рис. 27 б).
| Рис. 27 а. Продовольствие
|
| Рис. 27 б. Качественные товары
|
Дата добавления: 2015-11-26; просмотров: 1603;
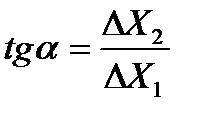 ;
;  ;
; 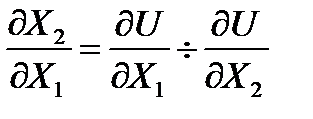 , т.е. предельная норма замещения равна обратному соотношению предельных полезностей благ.
, т.е. предельная норма замещения равна обратному соотношению предельных полезностей благ.
 ;
; (рис. 23).
(рис. 23).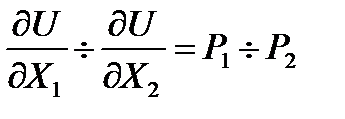 ,
,  отсюда
отсюда 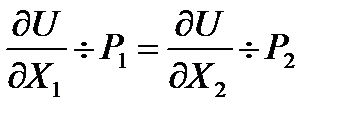 , т.е. мы пришли к эквамаржинальному принципу, по которому рациональный потребитель распределяет свой денежный доход таким образом, чтобы предельные полезности приобретаемых им благ, отнесенные к цене этих благ, были равными.
, т.е. мы пришли к эквамаржинальному принципу, по которому рациональный потребитель распределяет свой денежный доход таким образом, чтобы предельные полезности приобретаемых им благ, отнесенные к цене этих благ, были равными.