Добавление нового ограничения
Пусть в математической модели задачи (1-3) появилось новое ограничение
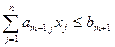
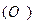

Возможны две ситуации:
· Если прежнее оптимальное решение удовлетворяет новому ограничению, то это решение оптимальное и для измененной задачи: 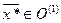 .
.
· Если прежнее оптимальное решение не удовлетворяет новому ограничению 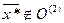 , то в таком случае прежнее оптимальное решение является базисным недопустимым решением и является псевдо-планом. Поэтому решение новой задачи может быть получено двойственным симплексным методом.
, то в таком случае прежнее оптимальное решение является базисным недопустимым решением и является псевдо-планом. Поэтому решение новой задачи может быть получено двойственным симплексным методом.
Для этого требуется новое ограничение привести к виду уравнения.
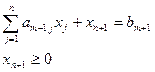
Включим новое ограничение в оптимальную симплекс-таблицу. Но прежде исключим из этого уравнения базисные переменные, чтобы в симплекс-таблице столбцы при базисных переменных были единичными.
Пример:
В задаче о работе ЦБК учтем ограничения на кислотные выбросы в атмосферу. Известно, что по первой технологии за 1 смену выбрасывается 1 кг кислотных выбросов, по второй – 3 кг. При этом предельно допустимые годовые нормы выброса составляют 360 кг.
В математической модели появится новое ограничение
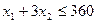 ,
,
а вся система ограничений примет вид
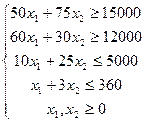
Проверим, удовлетворяет ли прежнее оптимальное решение 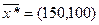 новому ограничению:
новому ограничению:
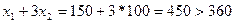
Ограничение не выполняется.
Преобразуем его к виду уравнения, введя балансовую переменную x6
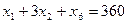
Заменим в этом уравнении базисные переменные x1, x2 их значениями через свободные из оптимальной симплекс-таблицы
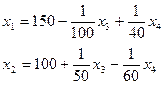
Уравнение примет вид
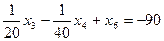
Включаем его в оптимальную симплекс-таблицу и решаем далее двойственным симплекс-методом
| Св | Бп | x1 | x2 | x3 | x4 | x5 | x6 | b |
| x2 | -1/50 | 1/60 | ||||||
| x1 | 1/100 | -1/40 | ||||||
| x5 | 2/5 | -1/6 | ||||||
| x6 | 1/20 | -1/40 | -90 | |||||
| F | -7/5 | -1/2 | ||||||
| x2 | 1/75 | 2/3 | ||||||
| x1 | 1/25 | -1 | ||||||
| x5 | 1/15 | -20/3 | ||||||
| x4 | -2 | -40 | ||||||
| F | -12/5 | -20 |
На следующей итерации получаем новое оптимальное решение
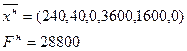
В новых условиях комбинат должен работать 240 смен по первой технологии, 40 смен по второй. Расход древесины возрастет до 28800 м3.
Дата добавления: 2016-01-11; просмотров: 1564;
