Изменение коэффициентов критерия

Влияние изменения коэффициентов критерия на оптимальное решение задачи хорошо видно на графике в пространстве двух управляемых параметров. Оптимальное решение не меняется, если вектор коэффициентов критерия (градиент функции) меняется в конусе градиентов активных ограничений.

Если меняется только коэффициент 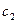(пусть это цена второго вида продукции), то

– при 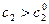оптимальное решение переходит в другую угловую точку области допустимых решений.

– при 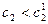оптимальное решение также меняется.

– при 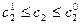оптимальное решение остается неизменным.

Как найти оптимальное решение задачи с измененными коэффициентами критерия, используя оптимальную симплекс-таблицу исходной задачи?

Пусть, для простоты, меняется только один коэффициент критерия. Будем отдельно рассматривать два случая:

– Меняется коэффициент критерия при свободной переменной оптимального плана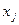

– Меняется коэффициент критерия при базисной переменной оптимального плана :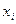

Симплекс-таблица оптимального плана 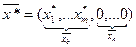имеет вид

		c1	c2	---	cm	cm+1	---	cj	---	cn
Св	Бп	x1	x2	---	xm	xm+1	---	xj	---	xn	b
с1	x1			---			---		---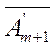
---	---	---	---	---	---
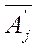
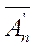
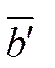
сm	xm			---
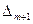
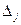
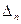
	F			---			---		---		F(x*)