Добавление новой переменной
Пусть в математической модели (1-3) появилась новая переменная 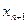
|
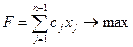
|
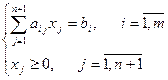
В задаче объемного планирования это означает возможность производить новый вид продукции с известными затратами ресурсов и известным доходом от единицы продукции. Сохранится ли прежнее оптимальное решение? Если нет, то как найти новое оптимальное решение?
Если в исходной задаче появляется новая переменная, то в двойственной задаче появляется новое ограничение
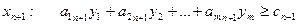 (6)
(6)
или 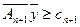
Вектор 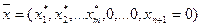 – прежнее оптимальное решение с нулевой n+1-ой компонентой является допустимым решением новой задачи (1’-3’). Если выполняется условие (6), то вектор
– прежнее оптимальное решение с нулевой n+1-ой компонентой является допустимым решением новой задачи (1’-3’). Если выполняется условие (6), то вектор 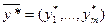 – прежний вектор оптимальных двойственных оценок – допустимое решение двойственной к (1’-3’) задачи. Соотношения дополняющей нежесткости для этих двух решений пополнились условием
– прежний вектор оптимальных двойственных оценок – допустимое решение двойственной к (1’-3’) задачи. Соотношения дополняющей нежесткости для этих двух решений пополнились условием
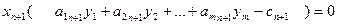
и выполняются за счет 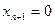 . Значит, по второй теореме двойственности,решение
. Значит, по второй теореме двойственности,решение 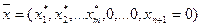 – оптимальное для новой задачи.
– оптимальное для новой задачи.
Этому выводу можно дать экономическое обоснование. Выполнение условия (6) означает, что затраты на единицу новой продукции превышают доход. Значит, такую продукцию производить невыгодно, 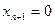 , прежнее оптимальное решение не меняется.
, прежнее оптимальное решение не меняется.
Если ограничение (6) не выполняется, затраты на единицу новой продукции меньше дохода, 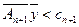 , то такую продукцию следует производить, объем производства нужно увеличивать.
, то такую продукцию следует производить, объем производства нужно увеличивать.
Для получения нового оптимального решения следует дополнить прежнюю оптимальную симплекс-таблицу новым столбцом
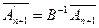 ,
,
а оценку переменной 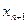 найти как разность левой и правой части ограничения (6) двойственной задачи
найти как разность левой и правой части ограничения (6) двойственной задачи
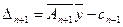
В полученной симплекс-таблице признак оптимальности не выполняется ( 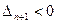 ), переменную
), переменную 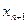 нужно вводить в список базисных и далее решать задачу симплекс-методом.
нужно вводить в список базисных и далее решать задачу симплекс-методом.
Пример:
Предположим, что у ЦБК появилась возможность работать по третьей технологии с расходом за смену 103 кубометра древесины, производительностью в смену 60 тонн целлюлозы, 40 центнеров лигнитов и 20 килограммов отравляющих веществ.
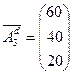 ,
, 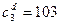 .
.
Обозначив 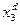 – время работы по третьей технологии, ищем решение в виде
– время работы по третьей технологии, ищем решение в виде 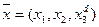 для новой математической модели
для новой математической модели
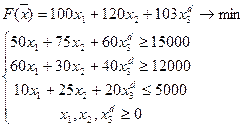 (7)
(7)
Новая переменная порождает в двойственной задаче новое ограничение
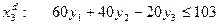 (8)
(8)
Проверим, удовлетворяет ли этому ограничению вектор оптимальных двойственных оценок 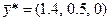 исходной задачи:
исходной задачи:
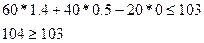
Ограничение (8) не выполняется, суммарная оценка полезности произведенной за смену продукции (104 м3) превышает затраты (103м3), значит прежнее решение 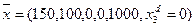 не является оптимальным.
не является оптимальным.
Для определения нового оптимального решения включим в прежнюю оптимальную симплекс таблицу столбец с переменной 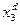 .
.
В исходную симплекс-таблицу новый вектор условий войдет в виде
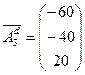 , так как менялись знаки в первых двух уравнениях (см. раздел 5.5). В оптимальной симплекс-таблице он преобразуется к виду
, так как менялись знаки в первых двух уравнениях (см. раздел 5.5). В оптимальной симплекс-таблице он преобразуется к виду
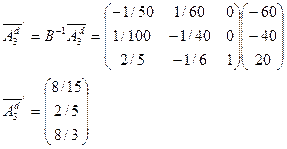
Оценка переменной 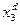 определится как разность левой и правой части ограничения двойственной задачи (8)
определится как разность левой и правой части ограничения двойственной задачи (8)
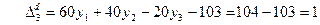
Оценка положительна, что нарушает условие оптимальности опорного плана. Решаем далее симплекс-методом
Исходная симплекс-таблица
| Св | Бп | x1 | x2 | x3 | x4 | x5 | x3d | b |
| x3 | -50 | -75 | -60 | -15000 | ||||
| x4 | -60 | -30 | -40 | -12000 | ||||
| x5 | ||||||||
| F | -100 | -120 | -103 | |||||
| Симплекс-таблица прежнего оптимального плана | ||||||||
| x2 | -1/50 | 1/60 | 8/15 | |||||
| x1 | 1/100 | -1/40 | 2/5 | |||||
| x5 | 2/5 | -1/6 | 8/3 | |||||
| F | -7/5 | -1/2 | ||||||
| Симплекс-таблица нового оптимального плана | ||||||||
| x3d | 15/8 | -3/80 | 1/32 | 375/2 | ||||
| x1 | -3/4 | 1/40 | -3/80 | |||||
| x5 | -5 | 1/2 | -1/4 | |||||
| F | -15/8 | -109/80 | -17/32 | 26812.5 |
На следующей итерации получим оптимальное решение новой задачи
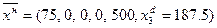
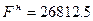
Комбинат должен работать 75 смен по первой технологии, 187.5 смен по третьей дополнительной технологии. При этом расход древесины будет наименьшим и составит 26812.5 кубометров.
Дата добавления: 2016-01-11; просмотров: 1179;
