Двойственный симплексный метод
Рассмотрим базисное недопустимое решение 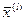 .
.
 Пусть все оценки на этом решении неотрицательные
Пусть все оценки на этом решении неотрицательные 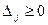 . Такое базисное решение называется псевдо-планом или псевдо-оптимальным решением. У него значение критерия лучше, чем у оптимального, но оно является недопустимым.
. Такое базисное решение называется псевдо-планом или псевдо-оптимальным решением. У него значение критерия лучше, чем у оптимального, но оно является недопустимым.
Для этого решения
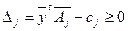 ,
, 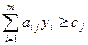 . А это означает, что псевдо-план исходной задачи соответствует опорному плану двойственной задачи:
. А это означает, что псевдо-план исходной задачи соответствует опорному плану двойственной задачи: 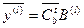 . При этом каждому псевдо-плану исходной задачи соответствует угловая точка двойственной.
. При этом каждому псевдо-плану исходной задачи соответствует угловая точка двойственной.
Двойственная задача может быть решена симплекс-методом без применения аппарата искусственного базиса.
 Двойственный симплекс-метод решения прямой задачи использует соответствующее решение двойственной задачи, но операции выполняются в симплекс-таблице исходной задачи. Перемещение происходит от одного псевдо-плана к другому с приближением к области. Когда очередное базисное решение станет допустимым, будет получено оптимальное решение.
Двойственный симплекс-метод решения прямой задачи использует соответствующее решение двойственной задачи, но операции выполняются в симплекс-таблице исходной задачи. Перемещение происходит от одного псевдо-плана к другому с приближением к области. Когда очередное базисное решение станет допустимым, будет получено оптимальное решение.
Если симплексный метод – метод последовательного улучшения плана (улучшаются планы 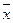 ), то двойственный симплекс-метод – метод последовательного улучшения оценок (улучшаются решения двойственной задачи – двойственные оценки
), то двойственный симплекс-метод – метод последовательного улучшения оценок (улучшаются решения двойственной задачи – двойственные оценки 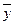 ).
).
Условия применимости двойственного симплекс-метода:
· в матрице условий задачи, записанной в канонической форме, должна быть единичная подматрица, при этом правые части ограничений не обязаны быть положительными.
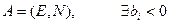
· все оценки должны быть неотрицательны, если задача на максимум, и неположительны, если задача на минимум.
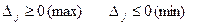
Итерации в двойственном симплекс-методе выполняются по следующим правилам:
· определяется переменная 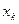 , выводимая из списка базисных. Она определяется по отрицательной компоненте
, выводимая из списка базисных. Она определяется по отрицательной компоненте 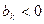 . Если их несколько, то лучше брать максимальную по модулю.
. Если их несколько, то лучше брать максимальную по модулю.
· определяется свободная переменная 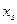 , вводимая в список базисных. При этом разрешающий столбец определяется по минимальному по модулю отношению оценок свободных переменных к отрицательным коэффициентам разрешающей строки.
, вводимая в список базисных. При этом разрешающий столбец определяется по минимальному по модулю отношению оценок свободных переменных к отрицательным коэффициентам разрешающей строки.
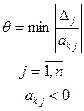
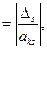
Это правило гарантирует, что новое базисное решение будет псевдо-планом.
· далее выполняются операции однократного замещения (как и в симплекс-методе) с разрешающим элементом 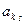 .
.
· процесс повторяется до тех пор, пока очередное базисное решение не станет допустимым.
Замечание: если в разрешающей строке нет отрицательных элементов, то область допустимых решений пуста.
Пример:
1. Содержательное описание.
Целлюлозно-бумажный комбинат (ЦБК) на берегу озера Байкал может работать по двум технологическим режимам. По первому режиму в течение смены расходуется 100 м3 древесины, производится 50 тонн целлюлозы, 60 центнеров лигнитов (вещества, используемые в химической промышленности) и сбрасывается в озеро 10 кг отравляющих веществ. По второму режиму в течение смены расходуется 120 м3 древесины, производится 75 тонн целлюлозы, 30 центнеров лигнитов, сбрасывается в озеро 25 кг отравляющих веществ. Годовой план производства составляет 15000 тонн целлюлозы, 1200 тонн лигнитов. Предельные годовые нормы выброса отравляющих веществ составляют 5 тонн. Определить годовой план работы ЦБК, требующий минимального расхода древесины.
2. Математическая модель.
2.1 Управляемые параметры.
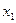 [см] – время работы (в сменах) по первой технологии;
[см] – время работы (в сменах) по первой технологии;
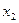 [см] – время работы (в сменах) по второй технологии;
[см] – время работы (в сменах) по второй технологии;
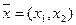 – годовой план работы.
– годовой план работы.
2.2 Ограничения.
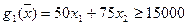 – годовое производство целлюлозы в тоннах должно быть не меньше плана;
– годовое производство целлюлозы в тоннах должно быть не меньше плана;
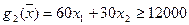 – годовое производство лигнитов в центнерах должно быть не меньше плана;
– годовое производство лигнитов в центнерах должно быть не меньше плана;
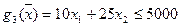 – годовой выброс отравляющих веществ в килограммах не должен превосходить предельно-допустимых норм выброса.
– годовой выброс отравляющих веществ в килограммах не должен превосходить предельно-допустимых норм выброса.
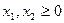 – время работы по каждой из технологий неотрицательно
– время работы по каждой из технологий неотрицательно
3. Формулировка цели.
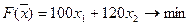 – годовой расход древесины должен быть минимален.
– годовой расход древесины должен быть минимален.
Получили следующую задачу линейного программирования
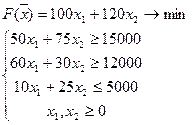 (1)
(1)
Приведем её к каноническому виду
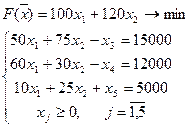
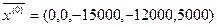 – очевидное базисное решение, но оно не является допустимым.
– очевидное базисное решение, но оно не является допустимым.
Обеспечим условия применения двойственного симплекс-метода. Сменим знаки левых и правых частей первых двух уравнений
|
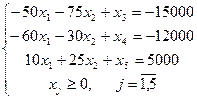
Занесем данные в симплекс-таблицу. Видим, что оценки переменных в последней строке первой симплекс-таблицы не положительны, то есть базисное решение 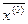 является псевдо-планом, условия применимости двойственного симплекс-метода выполняются.
является псевдо-планом, условия применимости двойственного симплекс-метода выполняются.
| Св | Бп | x1 | x2 | x3 | x4 | x5 | b |
| x3 | -50 | -75 | -15000 | ||||
| x4 | -60 | -30 | -12000 | ||||
| x5 | |||||||
| F | -100 | -120 | |||||
| x2 | 2/3 | -1/75 | |||||
| x4 | -40 | -2/5 | -6000 | ||||
| x5 | -20/3 | 1/3 | |||||
| F | -20 | -8/5 | |||||
| x2 | -1/50 | 1/60 | |||||
| x1 | 1/100 | -1/40 | |||||
| x5 | 2/5 | -1/6 | |||||
| F | -7/5 | -1/2 |
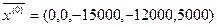 – псевдо-план.
– псевдо-план.
На первой итерации выбирается первая разрешающая строка (-15000<0) и второй разрешающий столбец (120/75<100/50). Выполняются операции однократного замещения. Получаем следующее приближение к области.
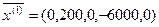
На второй итерации разрешающая строка вторая (-6000,0), разрешающий столбец первый (20/40=0.5< 8/5:2/5=4).
Следующее решение
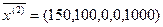 – допустимое базисное, значит оптимальное.
– допустимое базисное, значит оптимальное.
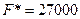
Экономическая интерпретация полученного решения: для обеспечения минимального расхода древесины нужно работать 150 смен по первой технологии, 100 смен по второй технологии, при этом расход древесины будет составлять 27000 м3. Производство целлюлозы и лигнитов совпадает с плановым (так как x3=x4=0), выброс отравляющих веществ на 1000 кг меньше предельно-допустимых норм выброса.
Построим двойственную задачу. Для применения правил построения двойственных задач необходимо согласовать знаки неравенств с типом критерия:
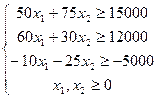 (3)
(3)
Введем переменные двойственной задачи:
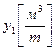 – оценка полезности 1 тонны целлюлозы;
– оценка полезности 1 тонны целлюлозы;
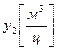 – оценка полезности 1 центнера лигнитов;
– оценка полезности 1 центнера лигнитов;
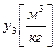 – оценка «полезности» 1 кг отравляющих веществ. Значение у3 на оптимальном плане будет показывать, на сколько изменится критерий при увеличении b3 на единицу (с -5000 до -4999). В терминах исходной задачи
– оценка «полезности» 1 кг отравляющих веществ. Значение у3 на оптимальном плане будет показывать, на сколько изменится критерий при увеличении b3 на единицу (с -5000 до -4999). В терминах исходной задачи 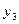 – это приращение расхода древесины от ужесточения (уменьшения) предельно допустимых норм выброса отравляющих веществ на один килограмм.
– это приращение расхода древесины от ужесточения (уменьшения) предельно допустимых норм выброса отравляющих веществ на один килограмм.
Тогда двойственная задача запишется в виде
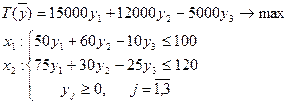 (4)
(4)
Найдем оптимальное решение двойственной задачи из оптимальной симплекс-таблицы прямой задачи:
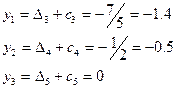 (5)
(5)
Казалось бы, полученное решение опровергает теорию получения оптимального решения двойственной задачи из оптимальной симплекс-таблицы прямой. Полученное решение 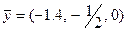 даже недопустимое – нарушаются условия неотрицательности в (4).
даже недопустимое – нарушаются условия неотрицательности в (4).
Действительно, (5) – это не оптимальное решение задачи (4), двойственной к задаче (3). Вектор 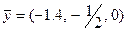 – это оптимальное решение задачи, двойственной к задаче (2). Именно эта задача представлена в исходной симплекс-таблице.
– это оптимальное решение задачи, двойственной к задаче (2). Именно эта задача представлена в исходной симплекс-таблице.
Хотя задачи (2) и (3) эквивалентны, имеют совпадающие области допустимых решений, но формы представления задач разные и двойственные к ним задачи будут отличаться не только формой, но и значением оптимальных решений. Однако оптимальные решения этих задач легко могут быть получены друг из друга.
Построим двойственную задачу к задаче (2):
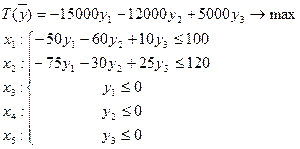 (6)
(6)
После замены переменных
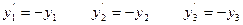
задача (6) обращается в задачу (4).
Таким образом, если из симплекс-таблицы получено оптимальное решение
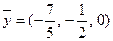 задачи, двойственной к задаче (2), то решение двойственной к задаче (3) может быть получено сменой знаков компонент решения:
задачи, двойственной к задаче (2), то решение двойственной к задаче (3) может быть получено сменой знаков компонент решения:
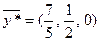
Экономический смысл двойственных переменных:
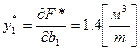 показывает, что при увеличении плана выпуска целлюлозы на 1 тонну расход древесины возрастет на 1.4 м3.
показывает, что при увеличении плана выпуска целлюлозы на 1 тонну расход древесины возрастет на 1.4 м3.
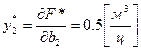 показывает, что при увеличении плана выпуска лигнитов на 1 центнер расход древесины возрастет на 0.5 м3.
показывает, что при увеличении плана выпуска лигнитов на 1 центнер расход древесины возрастет на 0.5 м3.
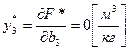 показывает, что при уменьшении годовых предельно допустимых норм выброса отравляющих веществ на 1 килограмм расход древесины не изменится. Действительно, на оптимальном решении ограничение по выбросу отравляющих веществ не активное, выброс (4000) не достигает предельной нормы (5000), поэтому уменьшение нормы не только на 1, но и на величину в пределах 1000 килограммов не повлияет на оптимальный план работы комбината.
показывает, что при уменьшении годовых предельно допустимых норм выброса отравляющих веществ на 1 килограмм расход древесины не изменится. Действительно, на оптимальном решении ограничение по выбросу отравляющих веществ не активное, выброс (4000) не достигает предельной нормы (5000), поэтому уменьшение нормы не только на 1, но и на величину в пределах 1000 килограммов не повлияет на оптимальный план работы комбината.
Полученные оценки влияния рассмотренных параметров на оптимальное значение критерия справедливы в области устойчивости двойственных оценок.
Дата добавления: 2016-01-11; просмотров: 2338;
