Построение областей устойчивости двойственных оценок

Интервал устойчивости двойственных оценок 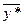к изменению компоненты вектора ограничений 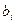– такой интервал изменения этой компоненты, внутри которого решение двойственной задачи не меняется.

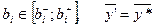
Для рассмотренной задачи найдем интервал устойчивости двойственных оценок к изменению запаса второго ресурса:

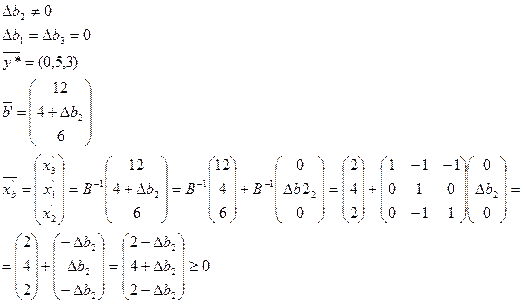
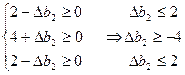
Получили интервал устойчивости в приращениях

,

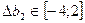А непосредственно интервал устойчивости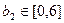

Это означает, что при уменьшении запасов второго ресурса до нуля или увеличении до 6 оценки всех ресурсов сохранят свои значения 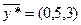, а приращение критерия можно найти по формуле

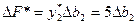
Построим область устойчивости двойственных оценок к изменению всех ресурсов.

Напомним, что область устойчивости двойственных оценок к изменению правых частей ограничений – множество значений правых частей ограничений, при которых двойственные оценки не меняются.

Область устойчивости 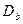определяется условиями

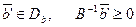
Подставляем сюда

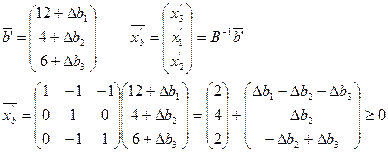
Для приращений ресурсов получаем систему неравенств

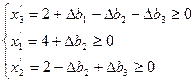
Неравенства (1) и определяют область устойчивости в трехмерном пространстве приращений ресурсов.

Если меняется только один ресурс, область устойчивости обращается в интервал устойчивости двойственных оценок к изменению этого ресурса.

Пусть меняется только второй ресурс:

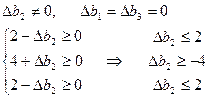
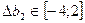
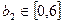– интервал устойчивости двойственных оценок 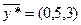к изменению второго ресурса.

Пусть меняется только третий ресурс:

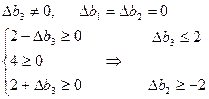
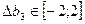
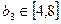– интервал устойчивости двойственных оценок 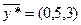к изменению третьего ресурса.

Построим область устойчивости двойственных оценок к одновременному изменению второго и третьего ресурсов:

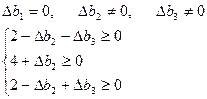
Из графика видно, что область устойчивости (в приращениях ресурсов) высекает на осях координат интервалы устойчивости. При изменении приращений ресурсов внутри этой области сохраняется неизменным (устойчивым) решение двойственной задачи 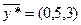, сохраняется базис оптимального плана 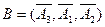, а компоненты (базисные) оптимального плана меняются по формулам .

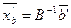Найдем новое оптимальное решение при конкретных изменениях ресурсов внутри области устойчивости.

Пусть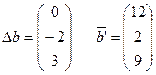

Тогда приращение оптимального значения критерия

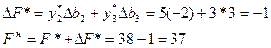
Базисные компоненты оптимального решения

,

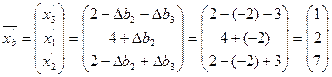а полный вектор нового оптимального решения

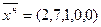
Экономическая интерпретация полученного решения:

При уменьшении запасов второго ресурса (катализатора) на 2 литра и одновременном увеличении длительности рабочей смены на 3 часа, по первой технологии следует работать 2 часа, по второй – 7 часов, при этом максимально возможный доход составит 37 тысяч рублей. Тонна первого ресурса останется неиспользованной.