Определение оптимального решения двойственной задачи из оптимальной симплекс-таблицы прямой
|
|
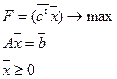
Оптимальное решение 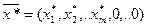 получено симплекс-методом,
получено симплекс-методом, 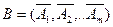 – базисная матрица оптимального решения.
– базисная матрица оптимального решения.
Оптимальное решение двойственной задачи (по первой теореме двойственности)
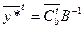 ,
,
элементы строки оценок в оптимальной симплекс-таблице прямой задачи вычисляются по формулам
|
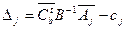
Подставляя (4) в (5) получим
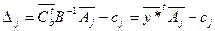
Памятуя о том, что ограничение двойственной задачи, соответствующее переменной 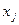 прямой задачи, имеет вид
прямой задачи, имеет вид
|
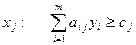 , или
, или 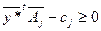 ,
,выводим из (6) важное свойство оценок
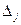 :
:
Оценка 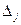 переменной
переменной 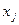 в симплекс-таблице равна разнице левой и правой части соответствующего ограничения двойственной задачи.
в симплекс-таблице равна разнице левой и правой части соответствующего ограничения двойственной задачи.
Из соотношения (6) легко найти компоненты оптимального решения двойственной задачи.
Действительно, пусть 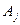 – единичный вектор с единицей в i-ой строке. В исходной симплекс-таблице всегда есть такие вектора.
– единичный вектор с единицей в i-ой строке. В исходной симплекс-таблице всегда есть такие вектора.

Оценка 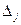 переменной
переменной 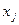 согласно (6) запишется
согласно (6) запишется
|
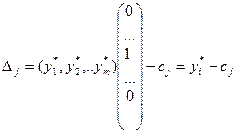 ,
,
откуда
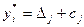
Таким образом, для определения компоненты 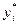 оптимального решения двойственной задачи следует в исходной симплекс-таблице выбрать единичный столбец
оптимального решения двойственной задачи следует в исходной симплекс-таблице выбрать единичный столбец 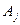 с единицей в i-ой строке. Тогда компонента
с единицей в i-ой строке. Тогда компонента 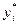 равна оценке
равна оценке 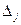 переменной
переменной 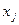 из оптимальной симплекс-таблицы плюс коэффициент критерия этой переменной
из оптимальной симплекс-таблицы плюс коэффициент критерия этой переменной
Пример:
Найдем оптимальное решение двойственной задачи к задаче раздела 5.2 о работе предприятия по двум технологиям.
Воспроизведем для наглядности решение симплекс-методом
| F | -M | ||||||
| Св | Бп | x1 | x2 | x3 | x4 | x5 | b |
| x3 | |||||||
| x4 | |||||||
| -M | x5 | ||||||
| F | -8-M | -3-M | -6M | ||||
| x3 | -2 | ||||||
| x1 | |||||||
| -M | x5 | -1 | |||||
| F | -3-M | 8+M | -2M+32 | ||||
| x3 | -1 | -1 | |||||
| x1 | |||||||
| x2 | -1 | ||||||
| F | 3+M | ||||||
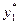
| 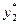
| 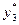
|
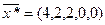
Единичная матрица в исходной симплекс таблице расположена в столбцах
3, 4, 5.
Оптимальное решение двойственной задачи будет находиться в строке оценок оптимальной симплекс-таблицы под единичной матрицей исходной симплекс-таблицы:
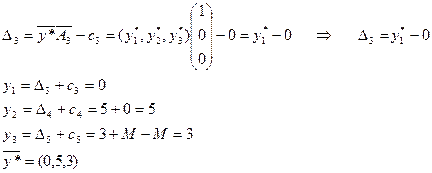
Дата добавления: 2016-01-11; просмотров: 910;
