Математические свойства пары взаимно двойственных задач
Исходная (прямая) задача
|
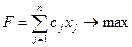
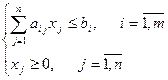
Исходная в матричном виде
|
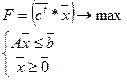
Двойственная задача
|
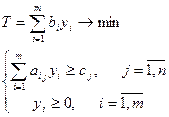
Двойственная задача в матричном виде
|
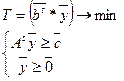
Лемма 1: двойственная задача к двойственной является исходной задачей.
Лемма 2 (основное неравенство теории двойственности): для любого допустимого решения прямой задачи и любого допустимого решения двойственной задачи критерий задачи максимизации не превосходит критерия задачи минимизации.
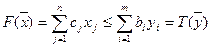 (7)
(7)
Доказательство:
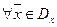 , для него выполняются (2) и (3).
, для него выполняются (2) и (3).
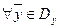 , для него выполняются (5) и (6).
, для него выполняются (5) и (6).
Покажем, что выполняется (7). Заменяя 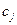 бóльшим значением из (5), затем
бóльшим значением из (5), затем 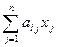 бóльшим значением из (2), получим
бóльшим значением из (2), получим
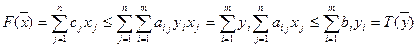

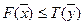
Теорема доказана.
Экономическая интерпретация основного неравенства теории двойственности: Суммарный доход на любом плане не может превзойти суммарной оценки используемых ресурсов при любых допустимых оценках.
|
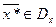 и
и 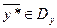 являются оптимальными для своих задач, если выполняется условие
являются оптимальными для своих задач, если выполняется условие
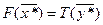
Доказательство:
Покажем, что в условиях леммы 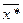 – оптимальное решение (
– оптимальное решение ( 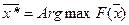 ). Выберем произвольное
). Выберем произвольное 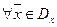 . По основному неравенству теории двойственности
. По основному неравенству теории двойственности 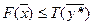 , по условию леммы
, по условию леммы 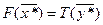 , значит
, значит 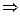
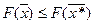 .
.
А это означает, что 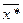 – оптимальное решение прямой задачи.
– оптимальное решение прямой задачи.
Аналогичным образом доказывается, что 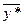 – оптимальное решение двойственной задачи.
– оптимальное решение двойственной задачи.
|
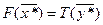
Доказательство приведем для прямой задачи в канонической форме:
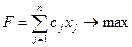
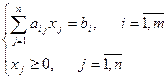
Двойственная задача
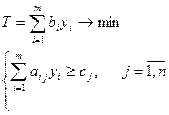
· Пусть 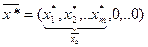 – опорное оптимальное решение прямой задачи,
– опорное оптимальное решение прямой задачи,
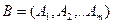 – его базисная матрица, тогда
– его базисная матрица, тогда
|
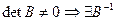 ,
,
и его базисные компоненты можно записать в виде
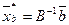
· По теореме 4 выполняется признак оптимальности
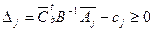 ,
, 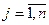 (11)
(11)
· Покажем, что оптимальное решение двойственной задачи может быть найдено в виде
|
|
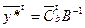
Подставим (12) в (11), получим
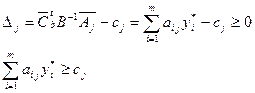
Неравенство (13) означает, что вектор 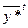 – допустимое решение двойственной задачи
– допустимое решение двойственной задачи
· Покажем, что для этого вектора выполняется условие (9):
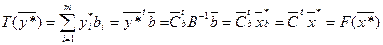
Тогда по лемме 3, если на двух допустимых решениях 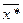 и
и 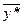 критерии равны
критерии равны 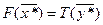 , то
, то 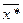 и
и 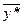 – оптимальные решения своих задач.
– оптимальные решения своих задач.
Тем самым доказано, что 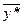 – оптимальное решение двойственной задачи.
– оптимальное решение двойственной задачи.
Теорема 1*: если исходная задача неразрешима из-за неограниченности критерия, то область допустимых решений двойственной задачи пуста.
Доказательство:
Предположим, что 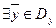 (область допустимых решений двойственной задачи не пуста). Тогда по лемме 2 для любого
(область допустимых решений двойственной задачи не пуста). Тогда по лемме 2 для любого 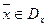
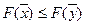 . Но по условию теоремы критерий исходной задачи не ограничен. Значит наше предположение не верно.
. Но по условию теоремы критерий исходной задачи не ограничен. Значит наше предположение не верно.
Тогда можно сделать вывод, что 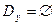 .
.
Теорема доказана.
Экономическая интерпретация первой теоремы двойственности: если существует оптимальный план производства, то существуют такие оценки ресурсов (производственных факторов), на которых достигается минимальная оценка затрат ресурсов и затраты полностью окупаются доходом, то есть производство эффективно – без потерь.
 Варианты разрешимости задач двойственной пары
Варианты разрешимости задач двойственной пары
Вариант 1: Обе задачи разрешимы.


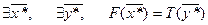
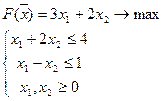

Построим двойственную задачу:
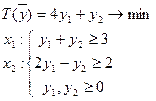
Вариант 2: Критерий одной задачи не ограничен, область допустимых решений другой задачи пуста.
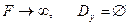 .
.
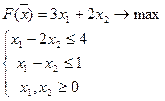
Построим двойственную задачу:


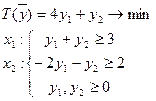
Вариант 3: Области допустимых решений обеих задач пусты.
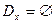 ,
, 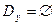 .
.
Построим двойственную задачу:
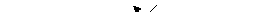
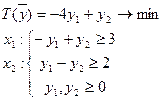
Таким образом, можно выделить следующие варианты разрешимости:
1. 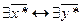
2. 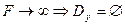
3. 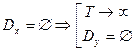
Следствие из первой теоремы двойственности: для разрешимости пары двойственных задач необходимо и достаточно, чтобы множество планов каждой из задач было не пустым.
Дата добавления: 2016-01-11; просмотров: 1699;
