Правила построения двойственной задачи
Для применения правил, необходимо в задаче на максимум записать все ограничения – неравенства со знаком 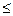 . В задаче же на минимум – со знаком
. В задаче же на минимум – со знаком 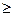 .
.
1. Количество переменных одной задачи совпадает с количеством ограничений другой задачи. Т.е. каждому ограничению одной задачи соответствует переменная другой. Ограничению-неравенству соответствует неотрицательная переменная, а ограничению-равенству – переменная произвольного знака.
2. Правые части ограничений одной задачи являются коэффициентами критерия другой.
3. Матрицы условий этих задач взаимно транспонированы, т.е. столбец матрицы условий одной задачи становится строкой другой.
4. Критерий одной задачи максимизируется, а другой минимизируется. Причем в задаче на максимум все ограничения – неравенства типа 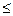 , а в задаче на минимум – типа
, а в задаче на минимум – типа 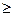 .
.
Пример:
Пусть исходная задача имеет вид:
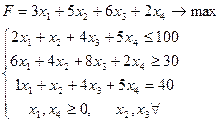
Построить двойственную задачу.
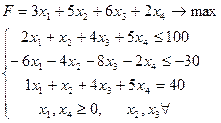
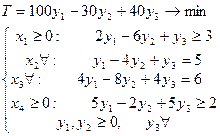
Покажем, что эти задачи взаимно двойственные. Для этого построим двойственную задачу к двойственной:
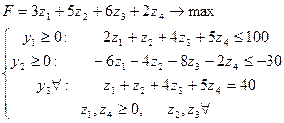
Действительно, полученная задача совпадает с исходной.
Дата добавления: 2016-01-11; просмотров: 819;
