Глава 4. Метод искусственного базиса

Построение начального опорного плана

Пусть задача линейного программирования дана в каноническом виде и правые части ограничений неотрицательны

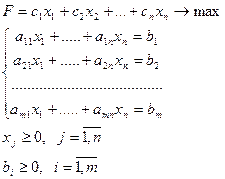
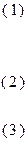
Если матраца условий содержит единичную подматрицу, опорный план очевиден.

В случае, когда матрица условий не содержит единичной подматрицы, для поиска опорного плана строится вспомогательная задача.

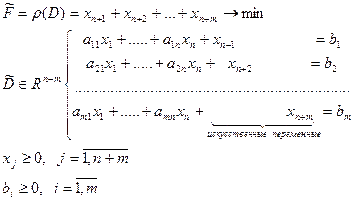
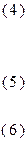
Опорный план этой задачи очевиден .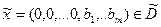

Область 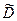содержит все решения исходной задачи.

Теорема 9: Пусть 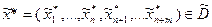оптимальное решение расширенной задачи (4)-(6). Если все искусственные переменные 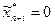, то это решение является опорным для исходной задачи. Если хотя бы одна искусственная переменная больше 0, тогда область допустимых решений исходной задачи пуста.

Вспомогательная задача всегда имеет оптимальное решение, так как функция 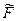ограничена снизу нулем и, значит, она достигает своего минимального значения.

Пример построения начального опорного плана

Предприятие работает по трем технологиям. По каждой технологии производится три продукта – A, B, C. По первой технологии за смену производится 1 тонна продукта A, 5 тонн продукта B и 2 тонны продукта С. По второй технологии за смену производится соответственно 2, 5, 3 тонн этих продуктов. По третьей технологии за смену производится 1, 2, 1 тонна продуктов. Продукта A должно быть произведено ровно 160 тонн, продукта B – не более 500 тонн, продукта С – не менее 190 тонн. Также известен доход за смену работы по каждой технологии – 6, 7 и 2 тыс. руб. соответственно. Найти время работы в сменах 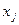по каждой из технологий, так чтобы суммарный доход был наибольшим.

Математическая модель задачи запишется в виде

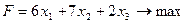
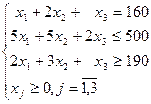
Приведем её к кононическому виду

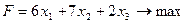
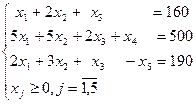
Для нахождения начального опорного плана строим вспомогательную задачу

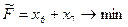
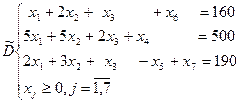
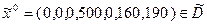
Построим симплекс-таблицу для этого опорного плана.

Св	Б.п	x1	x2	x3	x4	x5	x6	x7	b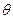
	x6
	x4
	x7					-1				63.333
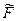
						-1
	x6	-1/3		1/3		2/3		-2/3	100/3
	x4	5/3		1/3		5/3		-5/3	550/3
	x2	2/3		1/3		-1/3		1/3	190/3
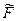
		-1/3		1/3		2/3		-5/3	100/3
	x5	-1/2		1/2			3/2	-1
	x4	5/2		-1/2			-5/2
	x2	1/2		1/2			1/2
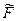
							-1	-1

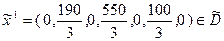
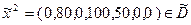
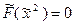
Решение 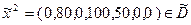является оптимальным решением вспомогательной задачи, так как в строке оценок симплекс-таблицы нет положительных оценок.

Замечание: если оптимальное решение вспомогательной задачи вырожденное, искусственные переменные равны нулю и при этом искусственная переменная является базисной, то необходимо заменить нулевую искусственную переменную любой свободной переменной так, чтобы разрешающий элемент был ненулевым.

Эти операции не реализованы в диалоговой системе решения и анализа задач линейного программирования IBLP, поэтому при использовании метода искусственного базиса в IBLP следует посмотреть на опорный план и выяснить, нет ли нулевой искусственной переменной в базисе. Если есть, то вывести её из списка базисных через блок “Базисные решения”.

Для получения оптимального решения исходной задачи следует исключить переменные x₆, x₇, сменить критерий на исходный и решать полученную задачу симплекс-методом.

Св	Б.п	x1	x2	x3	x4	x5	b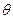
	x5	-1/2		1/2
	x4	5/2		-1/2
	x2	1/2		1/2
	F	-5/2		3/2
	x5			2/5	1/5
	x1			-1/5	2/5
	x2			3/5	-1/5
	F

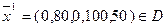
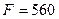
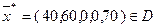– оптимальное решение.

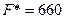
Таким образом, если работать 40 смен по первой технологии, 60 смен по второй технологии и не использовать третью технологию, то мы получим максимальный доход – 660 тыс. руб. При этом продукта B будет произведено по верхней границе, то есть 500 тонн, а продукта C будет производиться на 70 тонн больше, чем запланировано.