Этапы симплекс-метода
1. Проверка признака оптимальности ( 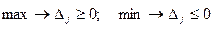 )
)
2. Если есть 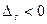 , то решение не оптимальное. Тогда выбираем столбец с минимальной оценкой. Его назовем разрешающим.
, то решение не оптимальное. Тогда выбираем столбец с минимальной оценкой. Его назовем разрешающим.
3. Разрешающая строка выбирается по минимальному отношению свободных членов к положительным коэффициентам разрешающего столбца. Базисная переменная, выражающаяся из этой строки, выходит из списка базисных переменных. Т.е. xk выходит, а xs входит.
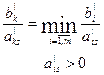
4. Текущая симплекс-таблица преобразуется по следующему правилу:
· разрешающая строка делится на разрешающий элемент:
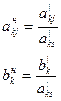
· разрешающий столбец заменяется единичным.
· все остальные элементы симплекс-таблицы могут быть пересчитаны по правилу четырехугольника:
Мысленно строится четырехугольник на диагонали, соединяющей искомый элемент с разрешающим. Тогда новое значение элемента равно прежнему значению минус произведение элементов на противоположной диагонали, деленное на разрешающий элемент.
Или новое значение элемента равно произведению элементов на главной диагонали минус произведение элементов на противоположной диагонали, и все это деленное на разрешающий элемент.
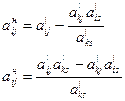
Замечание: Если в разрешающей строке был нулевой элемент, значит этот столбец не меняется; если в разрешающем столбце есть нулевой элемент, то соответствующая строка не меняется.
Варианты разрешимости задачи линейного программирования
Теорема 5: “О возможности увеличения критерия”.
Пусть 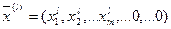 – невырожденный опорный план, существует оценка свободной переменной меньше нуля
– невырожденный опорный план, существует оценка свободной переменной меньше нуля 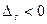 . Тогда план
. Тогда план 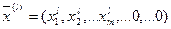 не оптимальный и существует решение с лучшим значением критерия.
не оптимальный и существует решение с лучшим значением критерия.
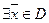
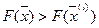
Для построения такого плана положим 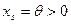 , тогда
, тогда
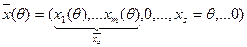 (15)
(15)
Существует такое малое 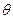 , что все базисные компоненты
, что все базисные компоненты 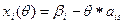 неотрицательны, то есть решение
неотрицательны, то есть решение 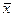 допустимое.
допустимое.
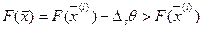
Теорема 6: “О возможности построения нового опорного плана”.
Если 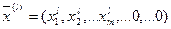 – невырожденный опорный план, существует
– невырожденный опорный план, существует 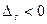 , среди коэффициентов текущей матрицы условий существуют
, среди коэффициентов текущей матрицы условий существуют 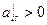 , то решение
, то решение 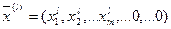 не оптимальное и существует новый опорный план с лучшим значением критерия.
не оптимальное и существует новый опорный план с лучшим значением критерия.
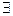
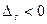 ,
, 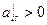
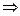
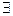
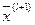
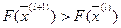
Действительно, построив план вида (15) и увеличивая 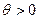 , заметим, что по крайней мере одна базисная переменная
, заметим, что по крайней мере одна базисная переменная 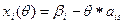 уменьшается. Когда одна из уменьшающихся базисных переменных обратится в 0, получим новый опорный план с лучшим значением критерия.
уменьшается. Когда одна из уменьшающихся базисных переменных обратится в 0, получим новый опорный план с лучшим значением критерия.
Теорема 7: “Условие неограниченности критерия”.
Если 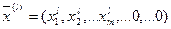 – невырожденный опорный план, существует
– невырожденный опорный план, существует 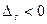 , среди коэффициентов текущей матрицы условий нет положительных
, среди коэффициентов текущей матрицы условий нет положительных 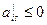 ,
, 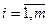 , то задача неразрешима из-за неограниченности критерия (
, то задача неразрешима из-за неограниченности критерия ( 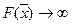 ).
).
Действительно, решение вида (15) остается допустимым при любом 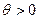 :
:
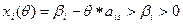 , а критерий неограниченно растет
, а критерий неограниченно растет 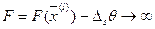
Теорема 8: “Признак альтернативного оптимального решения”.
Пусть 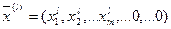 – невырожденный оптимальный план (выполняется признак оптимальности
– невырожденный оптимальный план (выполняется признак оптимальности 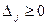 ,
, 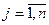 ), и существует оценка свободной переменной
), и существует оценка свободной переменной 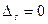 . Тогда оптимальный план не единственный и существует другой план с таким же значением критерия
. Тогда оптимальный план не единственный и существует другой план с таким же значением критерия 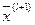 ,
, 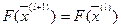 .
.
Действительно, на планах вида (15) критерий 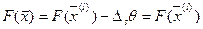 не изменяется, значит, все эти планы оптимальны.
не изменяется, значит, все эти планы оптимальны.
В таком случае оптимальные решения находятся на отрезке 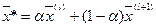 ,
, 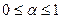 .
.
Дата добавления: 2016-01-11; просмотров: 1205;
