Базисные и опорные решения

Напомним, что допустимое решение задачи линейного программирования называется планом ( 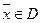). В силу условия (3) компоненты плана неотрицательны. Выделим отдельно положительные и отрицательные компоненты. Пусть первые k компонентположительны. Будем рассматривать вектора условий 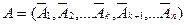при положительных и отрицательных компонентах плана.

Допустимое решение 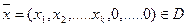называется опорным, если вектора условий при его положительных компонентах решения линейно-независимы.

Вектора линейно-зависимые, если (для трех векторов) 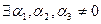такие, что выполняется равенство 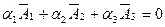; либо если определитель из этих векторов равен нулю.

Пример:

·

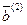
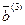
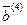
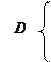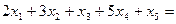
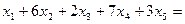
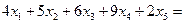
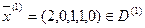
Проверим, опорное это решение или нет:

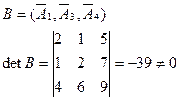
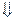
– опорное решение (невырожденное).

·

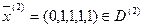
В трехмерном пространстве максимум только 3 вектора могут быть независимыми.

– не является опорным решением, так как векторы 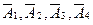линейно-зависимые. Значит, эта точка будет внутренней точкой области.

·

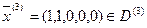
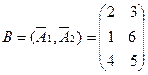
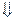
– опорное решение (вырожденное).

·

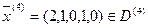
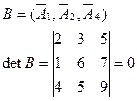
Так как определитель равен нулю, вектора линейно-зависимые.

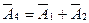
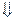
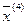– не является опорным решением.

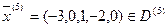· – базисное решение.

Положительные компоненты опорного решения называются базисными.

Вектора условий линейных компонентов могут быть базисом в пространстве.

Базис 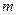- мерного пространства – совокупность любых 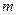линейно-независимых векторов .

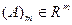Опорное решение называется невырожденным, если количество положительных компонент равно числу линейно-независимых ограничений (k=m).

Опорное решение называется вырожденным, если количество положительных компонент меньше числа линейно-независимых ограничений (k<m).

Нулевые переменные невырожденного опорного решения называются свободными.

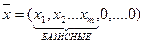
Матрица, состоящая из векторов при положительных компонентах невырожденного опорного плана, называется базисной.

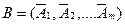
Базисное решение – решение системы уравнений (2) 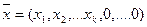, если вектора условий при его ненулевых компонентах линейно-независимые.

Базисная матрица – матрица из 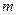линейно-независимых векторов условий, содержащая все вектора условий при ненулевых компонентах. Она всегда квадратная.

Базисная матрица невырожденного решения определяется однозначно, а базисная матрица вырожденного – неоднозначно.

Для определения базисного решения нужно выбрать произвольные 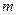переменных , вычислить определитель B из векторов условий этих переменных. Если 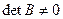, то занулить остальные переменные. Тогда для базисных переменных получим систему уравнений:

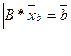
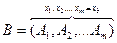
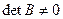
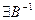
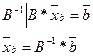
Максимальное количество базисных решений равно .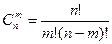

Опорное решение – допустимое базисное решение. Для поиска опорных решений можно перебрать все базисные решения и выбрать из них допустимые (с неотрицательными компонентами).

Теорема 3: опорные решения задачи ЛП совпадают с угловыми точками области допустимых решений.

Доказательство теоремы смотри в [8].