Свойства области допустимых решений
Пусть дана задача в канонической форме:
|
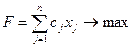
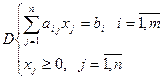
Пусть все уравнения линейно-независимые.
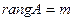
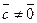
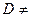 ø
ø
И пусть есть несколько 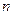 - мерных векторов
- мерных векторов 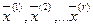 .
.
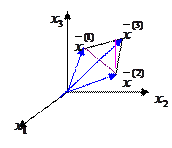
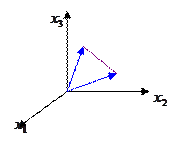
Выпуклая оболочка 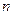 - мерных векторов – множество точек вида:
- мерных векторов – множество точек вида:
|
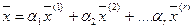
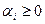 ,
, 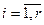 ,
, 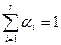
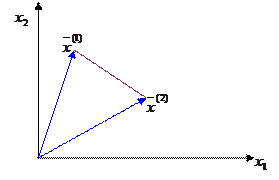
Выпуклая линейная комбинация двух векторов называется отрезком.
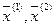
|
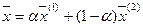 ,
, 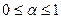
| Двумерное пространство | Трехмерное пространство |
|      
|
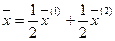
| 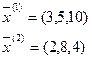
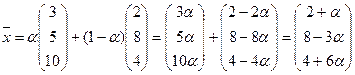
|
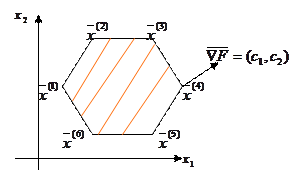
Область 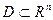 называется выпуклой, если вместе с любыми двумя своими точками она содержит отрезок, соединяющий их.
называется выпуклой, если вместе с любыми двумя своими точками она содержит отрезок, соединяющий их.
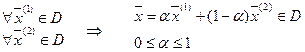 | |||
 |
Теорема 1: Область допустимых решений 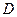 задачи ЛП выпуклая.
задачи ЛП выпуклая.
Доказательство:
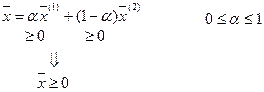 Пусть
Пусть 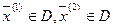 , т.е. для них выполняются (2) и (3).
, т.е. для них выполняются (2) и (3).
таким образом, условие (3) выполняется.
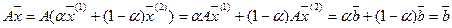
таким образом и условие (2) выполняется, произвольная точка отрезка принадлежит области D, то есть эта область выпукла.
Теорема доказана.
Точка 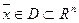 называется угловой (крайней), если не существует двух других точек области, на отрезке между которыми лежит эта точка.
называется угловой (крайней), если не существует двух других точек области, на отрезке между которыми лежит эта точка.
не 
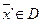 ,
, 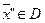 ,
,
|
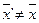 ,
, 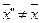 , таких, что
, таких, что 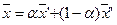 ,
, 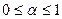

Лемма 1: Область допустимых решений 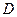 задачи ЛП является выпуклой линейной комбинацией своих угловых точек.
задачи ЛП является выпуклой линейной комбинацией своих угловых точек.
Таким образом, если найти все угловые точки, то любая точка внутри области записывается через уравнение (4).
Теорема 2: Оптимальное решение задачи ЛП достигается в одной из угловых точек области допустимых решений 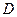 .
.
Покажем, что оптимальное решение не может быть внутри области.
Пусть 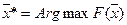 – внутренняя точка области. Тогда функция дифференцируема в этой точке:
– внутренняя точка области. Тогда функция дифференцируема в этой точке:
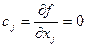
Так как в этой точке достигается максимум, то и производная здесь обратится в ноль.
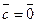
Но это противоречит условию, которое мы накладывали ранее, а именно 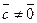 . Значит точка, в которой достигается оптимальное решение, лежит на границе области. Можно показать [8], что хотя бы одно оптимальное решение достигается в угловой точке.
. Значит точка, в которой достигается оптимальное решение, лежит на границе области. Можно показать [8], что хотя бы одно оптимальное решение достигается в угловой точке.
Дата добавления: 2016-01-11; просмотров: 1101;
