Графическое решение задач

Задача ЛП в симметричной форме (17) – (19) может быть решена графически, если пространство управляемых параметров содержит две или три переменные.

Пусть 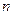= 2, тогда задача ЛП в симметричной форме выглядит так:

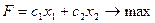
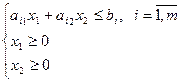
Изобразим область допустимых решений в пространстве управляемых параметров. Для этого рассмотрим множество точек, удовлетворяющих неравенству (35). Это будет полуплоскость, ограниченная прямой.

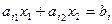Эта прямая делит все пространство на две полуплоскости. Для определения допустимой полуплоскости выбираем произвольную точку пространства, не лежащую на прямой (37) (лучше всего точку (0,0)), и подставляем её координаты в ограничение (35). Если ограничение выполняется, то полуплоскость, содержащая эту точку, допустимая.

Пересечение плоскостей образует область допустимых решений .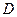

Поведение функции можно изобразить в пространстве управляемых параметров. Для этого достаточно построить семейство линий уровня функции. Линия уровня – это множество точек, в которых функция принимает постоянные значения.

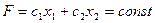(38)

Для задачи линейного программирования это прямые с разными константами в правой части уравнения (38).

Для построения линий уровня используем понятие градиента функции.

Градиент – это вектор частных производных функции.

= = ( )

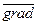
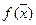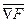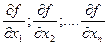Его можно вычислить в любой конкретной точке пространства переменных.

Свойства градиента функции

· Градиент функции, вычисленный в точке, перпендикулярен линии уровня функции, проходящей через эту точку.

· Направление градиента показывает направление максимального возрастания функции.

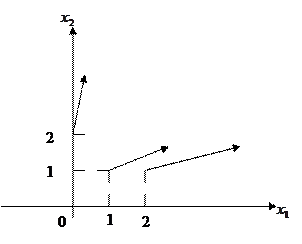Пример

=

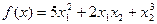
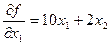
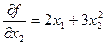
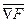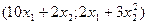
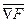
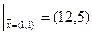
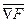
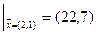
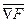
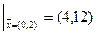
Линии уровня для нелинейных функций хорошо иллюстрируются линиями постоянной высоты над уровнем моря на географических картах. В задачах линейного программирования линии уровня – это параллельные прямые вида (38), а градиент функции – это вектор коэффициентов целевой функции. Он одинаков для всех точек пространства управляемых параметров.

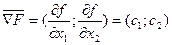
Для построения линий уровня в задаче линейного программирования можно выбрать произвольную точку области, построить в этой точке вектор градиента функции и перпендикулярно ему провести через выбранную точку линию уровня функции.

Для получения оптимального решения нужно перемещать линию уровня в направлении градиента до тех пор, пока она имеет общие точки с областью. Крайнее положение линии уровня называется опорной прямой (здесь вся область находится по одну сторону прямой и касается прямой в точке или отрезке). Общие точки опорной прямой с областью и являются оптимальными решениями.

Координаты оптимального решения находятся точно. Для этого нужно записать активные ограничения в виде равенств и решить совместно систему уравнений

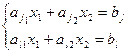
Пример

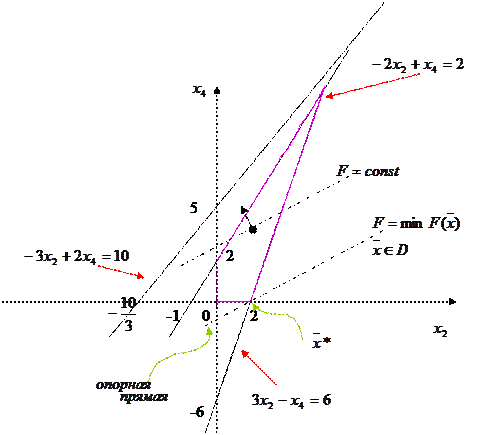
Решим графически задачу 2 из примеров раздела 1.3.

§

§

§

§

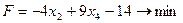
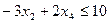
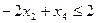
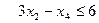
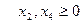
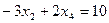
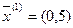
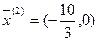
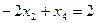
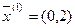
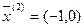
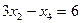
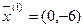
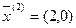
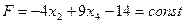
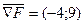
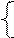
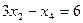
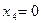
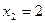
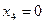
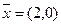– оптимальное решение двумерной задачи, в пространстве x₂,x₄.

Остальные компоненты решения можно найти из общего решения исходной системы уравнений.

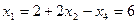
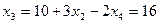
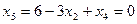
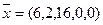­– полное оптимальное решение пятимерной задачи.

Графическое решение наглядно иллюстрирует свойства области допустимых решений задачи линейного программирования.