Закон и кривые Энгеля

Прусский статистик Эрнст Энгель еще в XIX в. обнаружил закономерность: по мере увеличения доходов человека, доля доходов, затрачиваемых на приобретение товаров первой необходимости, уменьшается, тогда как часть дохода, расходуемая на накопление и предметы роскоши, увеличивается.

Кривая Энгеля иллюстрирует зависимость между объемом потребления благ и доходом потребителя при неизменных ценах и предпочтениях. Она названа по имени немецкого экономиста и статистика Эрнста Энгеля (1821-1896), исследовавшего взаимосвязи между объемом покупаемого данным потребителем блага и величиной его дохода.

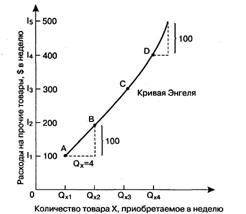
Рисунок 19 - Кривая Энгеля

На рисунке 19 денежный доход нанесен на вертикальной оси, а объем приобретенного за определенный период блага X - на горизонтальной оси. Данные кривые могут быть выведены для потребителя с определенными предпочтениями (вкусами) и при заданных ценах на благо X и другие блага.

Заметим, что кривые Энгеля схожи с кривыми спроса, поскольку они изображают соотношение между важным фактором, влияющим на спрос, и количеством приобретаемых благ.

Считается, что получить для некоторого блага кривую Энгеля достаточно несложно. Для этого нужно отложить доход на вертикальной оси и равновесное количество реализованного блага, соответствующего этому доходу, - на горизонтальной оси. Так, рисунке 19 кривая "доход-потребление" изображает, что когда потребитель, чьи кривые безразличия начерчены, имеет еженедельный доход в размере I1$, равновесное количество приобретаемого блага X составляет QX1 единиц в неделю. Это обозначено точкой А. Точка В соответствует точке Е2, для которой доход равен I2 $ в неделю и потребляемый объем X равен QX2.

Точки С и D на кривой Энгеля соотносятся на кривой "доход-потребление" с точками Е3 и Е4 соответственно. Кривая Энгеля образуется посредством соединения всех точек, соответствующих различному доходу и связанному с ним равновесному количеству покупок благ X. Кривая Энгеля для нормального товара имеет положительный наклон, поскольку увеличение дохода всегда вызывает увеличение потребляемого объема такого блага.

Наклон кривой Энгеля может быть выражен как:

dI/dQx или (Изменение в доходе)/(Изменение количества покупок блага X)

Наклон кривой Энгеля, изображенной на рисунке 19, увеличивается по мере увеличения еженедельного дохода. Форма кривой Энгеля отражает информацию о способности покупок блага реагировать на изменения в доходах.

Кривая Энгеля для блага, которое потребляется безотносительно к уровню дохода покупателя, имеет форму вертикальной прямой (Рисунок - 20). На рисунке 20 показана кривая Энгеля для такого блага. Так, ваши расходы на мандариновый сок не зависят от ваших доходов. Если вы покупаете 5 литров сока в неделю, то и при увеличении дохода все равно будете покупать 5 литров сока в неделю. Итак, кривая Энгеля демонстрирует, что независимо от размера дохода вы приобретаете в неделю один и тот же объем сока, т. е. изменения в доходе не приводят к изменениям в объеме приобретаемого блага.

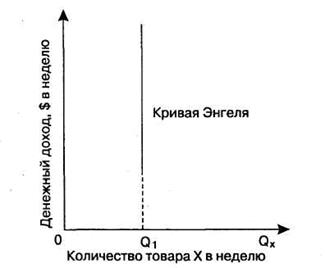
Рисунок 20 - Кривая Энгеля, отражающая эластичность покупок блага независимо от уровня доходов

Рисунок 21 показывает, что наклон кривой Энгеля уменьшается по мере увеличения доходов, при этом восприимчивость количества покупок блага X на изменение дохода возрастает, т. е. объем покупок увеличивается с увеличением доходов. Блага, которые приобретаются с увеличением доходов, часто рассматриваются как предметы роскоши. С уменьшением доходов объем покупки этих благ, наоборот, уменьшится.

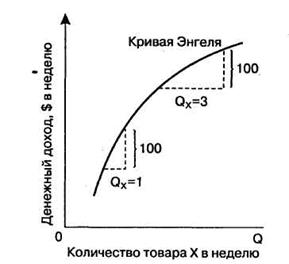
Рисунок 21 - Кривая Энгеля, отражающая эластичность покупок блага с изменением уровня доходов

Немецкий статистик А. Швабе отмечал ограниченность положений закона Энгеля. В частности, он указывал, что от доходов зависят тенденции изменения расходов на жилище. С. Струмилин на материалах пензенских бюджетов пришел к выводу, что доля расходов на питание находится в более тесной связи с размером семьи и возрастом ее членов.

Следовательно, связывать долю расходов семьи на питание с уровнем доходов, как это предлагал Энгель, некорректно, ибо должны учитываться и другие обстоятельства, на что указывали А. Швабе и С. Струмилин.