Внутренние силы в сечениях бруса и их определение
На основании гипотезы о сплошности материала между соседними частицами тела имеются определенные силы взаимодействия – внутренние силы. Эти силы сохраняют тело как единое целое при внешних воздействиях, препятствуя развитию деформаций.
 |
Для определения внутренних усилий пользуются методом сечений. Для этого элемент, находящийся в равновесии, мысленно рассекают сечением, перпендикулярным его оси, на две части А и В (рис. 1.7).
 Рассмотрим в равновесии часть А элемента (рис. 1.7 а). Со стороны отброшенной части В на нее действуют внутренние силы, распределенные по всему сечению. Из теоретической механики известно, что эта нагрузка может быть приведена к главному вектору
Рассмотрим в равновесии часть А элемента (рис. 1.7 а). Со стороны отброшенной части В на нее действуют внутренние силы, распределенные по всему сечению. Из теоретической механики известно, что эта нагрузка может быть приведена к главному вектору  и главному моменту
и главному моменту  (рис. 1.7 в).
(рис. 1.7 в).
Разложим главный вектор  и главный момент
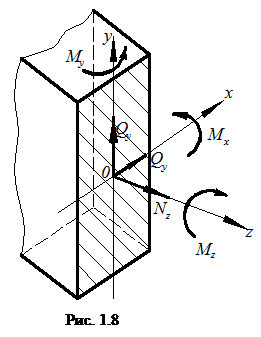
и главный момент  по осям координат x , y , и z (рис 1.8).
по осям координат x , y , и z (рис 1.8).
 (Qx, Qy, Nz)
(Qx, Qy, Nz)  (Mx, My, Mz).
(Mx, My, Mz).  (Mx, My, Mz).
(Mx, My, Mz).
Для нахождения этих шести составляющих имеем шесть уравнений статики:
| 1. ΣFx = 0 → Qx | 4. Σmx = 0 → Mx |
| 2. ΣFy = 0 → Qy | 5. Σmy = 0 → My |
| 3. ΣFz = 0 → Nz | 6. Σmz = 0 → Mz |
Внутренними усилиями или внутренними силовыми факторами называются величины, полученные в результате разложения главного вектора и главного момента по осям координат.
Qx, Qy - поперечные силы,
Nz - продольная сила,
Mx, My - изгибающие моменты,
Mz - крутящий момент.
В зависимости от того, какой внутренний силовой фактор действует в поперечном сечении элемента, будем иметь соответствующий вид деформации (рис.1.9 а, b, с, d, е):
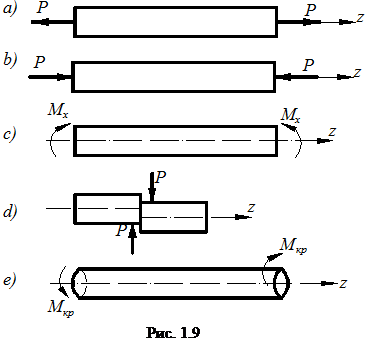
растяжение
сжатие
изгиб
сдвиг
кручение
Дата добавления: 2015-12-11; просмотров: 1375;
