Осевые, центробежный и полярный моменты инерции. Понятие о радиусах инерции и моментах сопротивления

Интегралы вида

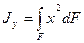, (2.5)

называются осевыми моментами инерции относительно осей х и у. Их значения всегда положительные.

Интеграл вида:

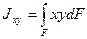(2.6)

называется центробежным моментом инерции. Он может принимать разные знаки и может быть равным нулю. Оси, относительно которых центробежный момент инерции равен нулю, называются главными осями. А если они проходят ещё и через центр тяжести сечения, то они будут главными центральными осями. Таким образом, основной задачей данного раздела сопротивления является материалов приобрести навык при вычислении осевых моментов инерции относительно главных центральных осей.

И далее, интеграл вида:

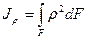(2.7)

описывает полярный момент инерции. Из (рис. 2.1) следует, что . Тогда полярный момент инерции

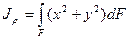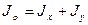или , (2.8)

т.е. полярный момент инерции, заданного сечения равен сумме осевых моментов инерции.

В частном случае для круглого сечения

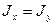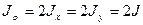; (2.9)

Приведенные осевые моменты инерции применяют при вычислении осевых радиусов инерции

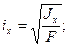
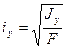(2.10)

Отношение осевых моментов инерции J_x, J_y к координатам наиболее удаленных точек по осям у_max и х_max называется осевыми моментами сопротивления, т.е:

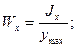
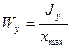, (2.11)

где 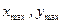- координаты наиболее удаленных точек в системе главных центральных осей.

Все эти геометрические характеристики будут использованы при выводе всех расчетных формул сопротивления материалов по оценке прочности, жесткости и устойчивости элементов конструкций.