Статические моменты площади. Центр тяжести сечения

Рассмотрим плоское сечение произвольной формы, связанное с прямоугольной декартовой системой координат х0у (рис. 2.1). Разобьём его на элементарные площадки линиями параллельными осям координат. Рассмотрим одну из таких площадок размером dFс координатами её центра тяжести х и у. Самой простой геометрической характеристикой сечения является его площадь F, определяемая интегралом:

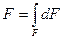(2.1)

где dF –дифференциал площади поперечного сечения бруса (рис. 2.1).

Интегралы вида

= , (2.2)

называются статическими моментами площади сечения относительно осей x, y, соответственно.

При этом S_x и S_y могут быть положительными, отрицательными и равными нулю. Оси, относительно которых статические моменты площади и 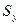равны нулю, называются центральными осями.

На основании теоремы о среднем (рис. 2.2) определенного интеграла формулы (2.2) можно записать так:

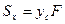; (2.3)

Отсюда, координаты центра тяжести сечения.

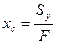, (2.4)

Для сечения, составленного из простейших фигур с площадями , координаты центра тяжести определяются по формулам:

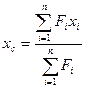
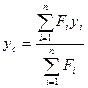(2.4*)

Здесь координаты центров тяжестей каждой составляющей фигуры в системе предварительно выбранных вспомогательных осей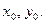

Пример 2.1.

Определим координату центра тяжести треугольника с высотой h, основанием b (рис. 2.3).

Для решения задачи воспользуемся формулами (2.4). Выберем случайную ось . Статический момент площади относительно вспомогательной оси найдем непосредственным интегрированием выражения:

= (а)

На расстоянии у от этой оси выделим элементарную площадку dF высотой dy. Тогда дифференциал площади

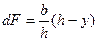
Статический момент площади относительно вспомогательной оси (а)

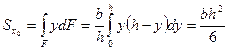
Координата центра тяжести треугольника

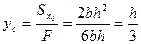
Следовательно, центр тяжести треугольника находится на расстоянии треть высоты от его основания.