Линейная множественная модель

Предположим, что функциональная структура ящика снова имеет линейную зависимость, но количество входных сигналов, действующих одновременно на объект, равно 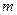(см. рис. 5.9):

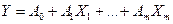
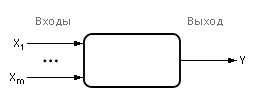
Рис. 5.9. Обозначение многомерного черного ящика на схемах

Так как подразумевается, что мы имеем экспериментальные данные о всех входах и выходах черного ящика, то можно вычислить ошибку между экспериментальным 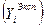и теоретическим 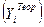значением 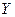для каждой 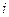-ой точки (пусть, как и прежде, число экспериментальных точек равно ):

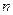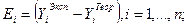
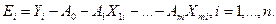
Минимизируем суммарную ошибку :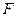

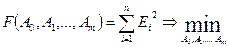
Ошибка 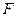зависит от выбора параметров 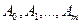. Для нахождения экстремума приравняем все частные производные 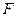по неизвестным 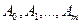к нулю:

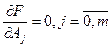
Получим систему из 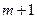уравнения с 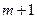неизвестными, которую следует решить, чтобы определить коэффициенты линейной множественной модели 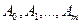. Для нахождения коэффициентов методом Крамера представим систему в матричном виде:

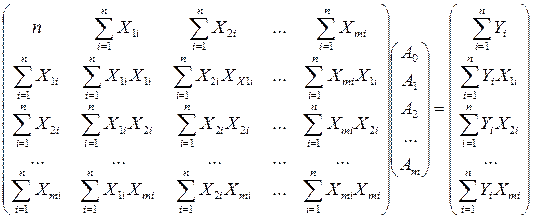
Вычисляем коэффициенты .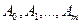

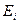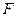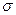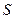Далее, по аналогии с одномерной моделью, для каждой точки вычисляется ошибка ; затем находится суммарная ошибка и значения и с целью определить, принимается ли выдвинутая гипотеза о линейности многомерного черного ящика или нет.

При помощи подстановок и переобозначений к линейной множественной модели приводятся многие нелинейные модели.